题目内容
观察以下等式：32-12=8，52-12=24，72-12=48，92-12=80，…由以上规律可以得出第n个等式为 ．
考点：规律型：数字的变化类
专题：规律型
分析：通过观察可发现两个连续奇数的平方差是8的倍数，第n个等式为：（2n+1）2-12=4n（n+1）．
解答：解：通过观察可发现两个连续奇数的平方差是8的倍数，
第n个等式为：（2n+1）2-12=4n（n+1）．
故答案为：（2n+1）2-12=4n（n+1）．
第n个等式为：（2n+1）2-12=4n（n+1）．
故答案为：（2n+1）2-12=4n（n+1）．
点评：此题考查了数字的变化类，通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题是应该具备的基本能力．
练习册系列答案
相关题目
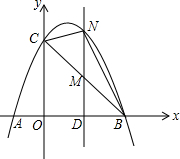如图，已知抛物线经过点A（-1，0）、B（3，0）、C（0，3）三点．
如图，在?ABCD中，点E、F分别在AD、BC上，且AE=CF．
如图，在△ABC中，D为BC上一点，DE∥AC交AB于E点，DF∥AB交AC于F点，当AD满足条件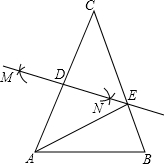
如图，在△ABC中，AC=BC，∠B=70°，分别以点A、C为圆心，大于
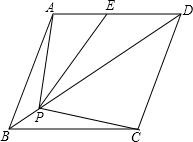菱形ABCD的边长为2，∠ABC=60°，E是AD边中点，点P是对角线BD上的动点，当AP+PE的值最小时，PC的长是
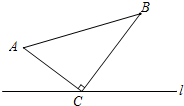如图，△ABC中，∠ACB=90°，AC=7cm，BC=1lcm．点M从A点出发沿A→C→B路径向终点运动，终点为B点；点N从B点出发沿B→C→A路径向终点运动，终点为A点．点M和N分别以每秒1cm和3cm的运动速度同时开始运动，两点都要到达相应的终点时才能停止运动，分别过M和N作ME⊥l于E，NF⊥l于F．设运动时间为t秒，则当t=