题目内容
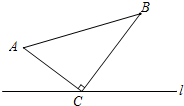 如图,△ABC中,∠ACB=90°,AC=7cm,BC=1lcm.点M从A点出发沿A→C→B路径向终点运动,终点为B点;点N从B点出发沿B→C→A路径向终点运动,终点为A点.点M和N分别以每秒1cm和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,则当t=
如图,△ABC中,∠ACB=90°,AC=7cm,BC=1lcm.点M从A点出发沿A→C→B路径向终点运动,终点为B点;点N从B点出发沿B→C→A路径向终点运动,终点为A点.点M和N分别以每秒1cm和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,则当t=考点:全等三角形的判定
专题:动点型,分类讨论
分析:易证∠MEC=∠CFN,∠MCE=∠CNF.只需MC=NC,就可得到△MEC与△CFN全等,然后只需根据点M和点N不同位置进行分类讨论即可解决问题.
解答:解:①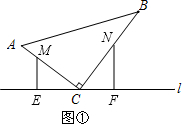 当0≤t<
当0≤t<
时,点M在AC上,点N在BC上,如图①,
此时有AM=t,BN=3t,AC=7,BC=11.
当MC=NC即7-t=11-3t,也即t=2时,
∵ME⊥l,NF⊥l,∠ACB=90°,
∴∠MEC=∠CFN=∠ACB=90°.
∴∠MCE=90°-∠FCN=∠CNF.
在△MEC和△CFN中,
.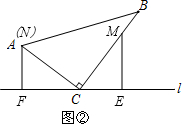
∴△MEC≌△CFN(AAS).
②当
≤t<7时,点M在AC上,点N也在AC上,
若MC=NC,则点M与点N重合,故不存在.
③当7<t<18时,点N停在点A处,点N在BC上,如图②,
当MC=NC即t-7=7,也即t=14时,
同理可得:△MEC≌△CFN.
综上所述:当t等于2或14秒时,以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等.
故答案为:2或14.
 当0≤t<
当0≤t<| 11 |
| 3 |
此时有AM=t,BN=3t,AC=7,BC=11.
当MC=NC即7-t=11-3t,也即t=2时,
∵ME⊥l,NF⊥l,∠ACB=90°,
∴∠MEC=∠CFN=∠ACB=90°.
∴∠MCE=90°-∠FCN=∠CNF.
在△MEC和△CFN中,
|

∴△MEC≌△CFN(AAS).
②当
| 11 |
| 3 |
若MC=NC,则点M与点N重合,故不存在.
③当7<t<18时,点N停在点A处,点N在BC上,如图②,
当MC=NC即t-7=7,也即t=14时,
同理可得:△MEC≌△CFN.
综上所述:当t等于2或14秒时,以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等.
故答案为:2或14.
点评:本题主要考查了全等三角形的判定以及分类讨论的思想,可能会因考虑不全面而出错,是一道易错题.

练习册系列答案
相关题目
 小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y km与已用时间x h之间的关系,则小敏、小聪行走的速度分别是( )
小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y km与已用时间x h之间的关系,则小敏、小聪行走的速度分别是( )| A、3km/h和4km/h |
| B、3km/h和3km/h |
| C、4km/h和4km/h |
| D、4km/h和3km/h |
下列实数0,0.3,
,
,π,0.
,6.1010010001中,无理数有( )
| ||
| 3 |
| 1 |
| 7 |
| • |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
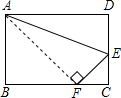 如图,折叠矩形,使点D落在BC边上的点F处,BC=10cm,AB=8cm,则FC=
如图,折叠矩形,使点D落在BC边上的点F处,BC=10cm,AB=8cm,则FC=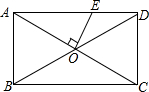 如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE⊥AC交AD于点E,则AE的长是
如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE⊥AC交AD于点E,则AE的长是