Question

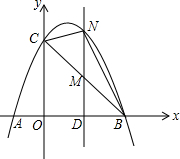如图，已知抛物线经过点A（-1，0）、B（3，0）、C（0，3）三点．
（1）求抛物线的解析式．
（2）点M是线段BC上的点（不与B，C重合），过M作MN∥y轴交抛物线于N，若点M的横坐标为m，连接NB、NC，是否存在m，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由．
（3）点P是x轴上方抛物线上一点，Q是x轴上一动点，若以A、C、P、Q为顶点的四边形为等腰梯形，则P的坐标是多少？请直接写出答案．

Answer 1

考点：二次函数综合题

专题：

分析：（1）用待定系数法求出抛物线解析式．
（2）利用S_△BNC=S_△MNC+S_△MNB列出方程，根据方程求出当m为

3

2

时，有最大值．
（3）①当CA=PQ，CP∥AB时，求出点P的坐标，②作GH⊥AC且平分AC，交AC于点H．连接CG交抛物线于点P．先求出点G的坐标，再求出直线GH的解析式，与抛物线的解析式联立．求出交点P的坐标．

解答：解：设抛物线解析式为：y=ax²+bx+c
∵抛物线经过点A（-1，0）、B（3，0）、C（0，3）三点，
∴

0=a-b+c 0=9a+3b+c 3=c

解得

a=-1 b=2 c=3

抛物线解析式为：y=-x²+2x+3，
（2）如图．

∵S_△BNC=S_△MNC+S_△MNB，
=

1

2

MN×（OD+DB）
=

1

2

MN•OB
∵OB=OC，
∴∠CBO=45°，
∵BD=3-m，
∴MN=-m²+2m+3-（3-m）=-m²+3m，
∴S_△BNC=

1

2

（-m²+3m）×3=-

3

2

（m-

3

2

）²+

27

8

（0＜m＜3），
∴当m=

3

2

时，△BNC的面积最大，最大值为

27

8

．
（3）①如图2，当CA=PQ，CP∥AB时，点Q与点B重合

∵抛物线解析式为：y=-x²+2x+3，
∴对称轴x=1
∵C（0，3），
∴P点的坐标为（2，3），
②如图3，作GH⊥AC且平分AC，交AC于点H．连接CG交抛物线于点P．过点P作PQ∥AC的得的四边形为等腰梯形．

∵A（-1，0）、C（0，3），
∴AC=

10

，
∴AH=

10

2

，
∵tan∠CAO=3，
∴HG=

3 10

2

，
∴AG=

( 10 2 )2+( 3 10 2 )2

=5，
∴G（4，0），
∵点C（0，3）
设直线CH的解析式为y=kx+b，
∴

0=4k+b 3=b

解得，

k=- 3 4 b=3

∴直线GH的解析式为y=-

3

4

x+3，
与抛物线解析式y=-x²+2x+3组成方程组得，

y=- 3 4 x+3 y=-x2+2x+3

解得，

x1=0 y1=3

，

x2= 11 4 y2= 15 16

∴P的坐标为（

11

4

，

15

16

），
综上所述点P（2，3）或（

11

4

，

15

16

）．

点评：本题主要考查了二次函数的综合题，解题的关键是分两种情况，分析以A、C、P、Q为顶点的四边形为等腰梯形，并求出点P的坐标．