题目内容
7.4张奖券中有2张是有奖的,甲、乙先后各抽一张.(1)甲中奖的概率是$\frac{1}{2}$;
(2)试用列树状图或列表法求甲、乙都中奖的概率.
分析 (1)由4张奖券中有2张是有奖的,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲、乙都中奖的情况,再利用概率公式即可求得答案.
解答 解:(1)∵4张奖券中有2张是有奖的,
∴甲中奖的概率是:$\frac{2}{4}$=$\frac{1}{2}$;
故答案为:$\frac{1}{2}$;
(2)设四张奖券分别为奖1、奖2、空1、空2,
列表得: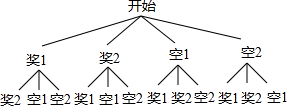
∵共有12种等可能结果,其中甲、乙都中奖的有2种情况.
∴P(甲、乙都中奖)=$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
18.下列运算正确的是( )
| A. | (x+y2)2=x2+y4 | B. | b6÷b2=b3 | C. | -a2+2a2=a2 | D. | (2y)2×(-y)=-2y3 |
15.我校举行了“建设宜居中山,关注环境保护”的知识竞赛,某班学生的成绩统计如下:
则该班学生成绩的众数和中位数分别是( )
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数 | 4 | 8 | 12 | 11 | 5 |
| A. | 70分,80分 | B. | 80分,80分 | C. | 90分,80分 | D. | 80分,90分 |
2. 将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是( )
将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是( )
 将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是( )
将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是( )| A. | 44° | B. | 45° | C. | 46° | D. | 54° |
12.已知一个正多边形一个外角是72°,则这个正多边形是( )
| A. | 四边形 | B. | 五边形 | C. | 六边形 | D. | 七边形 |
19.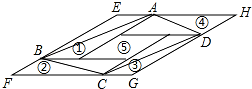 如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.
如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.
 如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.
如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.| A. | 45 | B. | 46 | C. | 47 | D. | 48 |
16.某公司根据市场计划调整投资策略,对A,B两种产品进行市场调查,收集数据如表:
其中m是待定常数,其值是由生产A的材料的市场价格决定的,变化范围是6≤m≤8,销售B产品时需缴纳$\frac{1}{20}$x2万元的关税,其中x为生产产品的件数,假定所有产品都能在当年售出,设生产A,B两种产品的年利润分别为y1、y2(万元),写出y1、y2与x之间的函数关系式,注明其自变量x的取值范围.
| 项目 产品 | 年固定成本 (单位:万元) | 每件成本 (单位:万元) | 每件产品销售价 (万元) | 每年最多可生产的件数 |
| A | 20 | m | 10 | 200 |
| B | 40 | 8 | 18 | 120 |
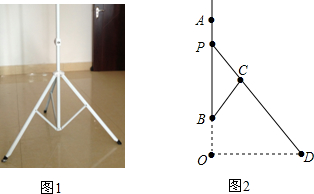
 如图,点B、C、E在同一条直线上,请你写出一个能使AB∥CD成立的条件:∠1=∠2.(只写一个即可,不添加任何字母或数字)
如图,点B、C、E在同一条直线上,请你写出一个能使AB∥CD成立的条件:∠1=∠2.(只写一个即可,不添加任何字母或数字)