题目内容
20．已知直角三角形两直角边分别是3和4，将这两边扩大到原来的两倍，则斜边的长为（ ）| A． | 5 | B． | 6 | C． | 8 | D． | 10 |
分析 求出扩大后的直角三角形的两直角边分别是6和8，由勾股定理即可得出答案．
解答 解：根据题意得：扩大后的直角三角形的两直角边分别是6和8，
由勾股定理，得斜边=$\sqrt{{6}^{2}+{8}^{2}}$=10．
故选：D．
点评 本题考查了勾股定理的运用．熟练掌握勾股定理是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
10．某体校的甲、乙两名体育生，在进行10米气手枪设计测试时，每人射击5次，甲体育生射中的环数（单位：环）为：8，6，7，7，7；乙体育生射中的环数（单位：环）为：6，5，9，7，8，则下列说法中不正确的是（ ）
| A． | 甲体育生此次射击成绩的众数为7环 | |
| B． | 乙体育生此次射击成绩的平均数为7环 | |
| C． | 甲体育生此次射击成绩的成绩比乙体育生的稳定 | |
| D． | 乙体育生此次射击成绩的中位数为6环 |
如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF，若∠1=72°，求∠2的度数．
8．化简（x+1）-（1-x）+（x-1）的结果是（ ）
| A． | x-1 | B． | 3x+1 | C． | 3x-3 | D． | 3x-1 |
15．一个数减去2等于-3，则这个数是（ ）
| A． | -5 | B． | -1 | C． | 1 | D． | 5 |
5．化简（1-$\frac{2}{x+1}$）÷$\frac{1}{{x}^{2}-1}$的结果是（ ）
| A． | （x+1）2 | B． | （x-1）2 | C． | $\frac{1}{（x+1）^{2}}$ | D． | $\frac{1}{（x-1）^{2}}$ |
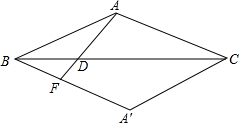如图：等腰三角形ABC中，∠ABC=20°，将△ABC沿BC向下翻折得到△A′BC．已知D为线段BC上一点．连接AD，并延长AD交A′B于点F，若∠BAD=∠ABC，BF=3，CD=5，那么△ACD的面积为$\frac{15}{4}\sqrt{3}$．
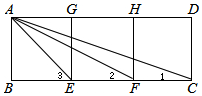如图，四边形ABEG、GEFH、HFCD都是边长相等的正方形