题目内容
8．化简（x+1）-（1-x）+（x-1）的结果是（ ）| A． | x-1 | B． | 3x+1 | C． | 3x-3 | D． | 3x-1 |
分析 原式去括号合并即可得到结果．
解答 解：原式=x+1-1+x+x-1=3x-1，
故选D
点评 此题考查了整式的加减，涉及的知识有：去括号法则与合并同类项法则，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
18．如果多项式y2+my+16是完全平方式，那么m的值为（ ）
| A． | 8 | B． | -8 | C． | ±4 | D． | ±8 |
19．
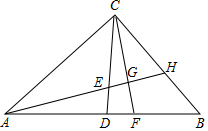如图，在△ABC中，∠ACB=90°，AC=BC，AB=4cm，CD是中线，点E、F同时从点D出发，以相同的速度分别沿DC、DB方向移动，当点E到达点C时，运动停止，直线AE分别与CF、BC相交于G、H，则在点 E、F移动过程中，点G移动路线的长度为（ ）
如图，在△ABC中，∠ACB=90°，AC=BC，AB=4cm，CD是中线，点E、F同时从点D出发，以相同的速度分别沿DC、DB方向移动，当点E到达点C时，运动停止，直线AE分别与CF、BC相交于G、H，则在点 E、F移动过程中，点G移动路线的长度为（ ）| A． | 2 | B． | π | C． | 2 | D． | $\frac{{\sqrt{2}}}{2}$π |
16．在一次函数y=-x+2的图象上的点是（ ）
| A． | （-1，4） | B． | （2，0） | C． | （1，0） | D． | （2，1） |
3．下列计算正确的是（ ）
| A． | a2+a3=a5 | B． | a6-a4=a2 | C． | x2•x3=x6 | D． | y3÷y=y2 |
13．在△ABC中，∠ACB=90°，BC=1，AC=2，则下列正确的是（ ）
| A． | sinA=$\frac{2\sqrt{5}}{5}$ | B． | tanA=$\frac{\sqrt{5}}{5}$ | C． | cosB=$\frac{\sqrt{5}}{5}$ | D． | tanB=$\frac{1}{2}$ |
20．已知直角三角形两直角边分别是3和4，将这两边扩大到原来的两倍，则斜边的长为（ ）
| A． | 5 | B． | 6 | C． | 8 | D． | 10 |
17．
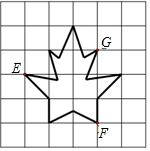如图所示，若点E的坐标为（-2，1），点F的坐标为（1，-1），则点G的坐标为（ ）
如图所示，若点E的坐标为（-2，1），点F的坐标为（1，-1），则点G的坐标为（ ）| A． | （1，2） | B． | （2，2） | C． | （2，1） | D． | （1，1） |
7．已知x与y之间的关系如表所示：
下面用x表示y的式子中，正确的是（ ）
| x | 1 | 2 | 3 | 4 | … |
| y | 0.6+3 | 0.6+6 | 0.6+9 | 0.6+12 | … |
| A． | y=0.6+x | B． | y=0.6+3x | C． | y=0.6×3+x | D． | y=0.6×3-x |