题目内容
11．
如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF，若∠1=72°，求∠2的度数．
分析 先根据平行线的性质，求得∠BEF的度数，直接角平分线的定义以及平行线的性质，即可得出∠2的度数．
解答 解：∵AB∥CD，
∴∠1+∠BEC=180°，
∵∠1=72°，
∴∠BEC=180°-72°=108°，
∵EG平分∠BEF，
∴∠BEG=$\frac{1}{2}$∠BEF=$\frac{1}{2}$×108°=54°，
又∵AB∥CD，
∴∠BEG=∠2，
∴∠2的度数为54°．
点评 本题主要考查了平行线的性质以及角平分线的定义的综合应用，解决问题的关键是运用：两直线平行，同旁内角互补；两直线平行，内错角相等．
练习册系列答案
相关题目
1．声音在空气中的传播速度是每秒340米，一种超音速飞机比声音的速度快$\frac{2}{5}$，求这种飞机的速度列式正确的是（ ）
| A． | 340+$\frac{2}{5}$ | B． | 340×（1+$\frac{2}{5}$） | C． | 340+340×$\frac{3}{5}$ | D． | 340×$\frac{2}{5}$ |
2．
如图，AB是⊙O的直径，CD是弦，∠ABC=65°，则∠D的度数为（ ）
如图，AB是⊙O的直径，CD是弦，∠ABC=65°，则∠D的度数为（ ）| A． | 130° | B． | 65° | C． | 35° | D． | 25° |
19．
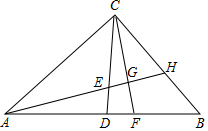如图，在△ABC中，∠ACB=90°，AC=BC，AB=4cm，CD是中线，点E、F同时从点D出发，以相同的速度分别沿DC、DB方向移动，当点E到达点C时，运动停止，直线AE分别与CF、BC相交于G、H，则在点 E、F移动过程中，点G移动路线的长度为（ ）
如图，在△ABC中，∠ACB=90°，AC=BC，AB=4cm，CD是中线，点E、F同时从点D出发，以相同的速度分别沿DC、DB方向移动，当点E到达点C时，运动停止，直线AE分别与CF、BC相交于G、H，则在点 E、F移动过程中，点G移动路线的长度为（ ）| A． | 2 | B． | π | C． | 2 | D． | $\frac{{\sqrt{2}}}{2}$π |
6．若|x+3|+|y-2|=0，则x+y的值为（ ）
| A． | 5 | B． | -5 | C． | -1 | D． | 1 |
16．在一次函数y=-x+2的图象上的点是（ ）
| A． | （-1，4） | B． | （2，0） | C． | （1，0） | D． | （2，1） |
3．下列计算正确的是（ ）
| A． | a2+a3=a5 | B． | a6-a4=a2 | C． | x2•x3=x6 | D． | y3÷y=y2 |
20．已知直角三角形两直角边分别是3和4，将这两边扩大到原来的两倍，则斜边的长为（ ）
| A． | 5 | B． | 6 | C． | 8 | D． | 10 |
10．
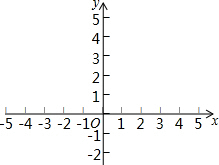问题：探究函数y=|x|-2的图象与性质．
小华根据学习函数的经验，对函数y=|x|-2的图象与性质进行了探究．
下面是小华的探究过程，请补充完整：
（1）在函数y=|x|-2中，自变量x可以是任意实数；
（2）如表是y与x的几组对应值．
①m=1；
②若A（n，8），B（10，8）为该函数图象上不同的两点，则n=-10；
（3）如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；
根据函数图象可得：
①该函数的最小值为-2；
②已知直线${y_1}=\frac{1}{2}x-\frac{1}{2}$与函数y=|x|-2的图象交于C、D两点，当y1≥y时x的取值范围是-1≤x≤3．
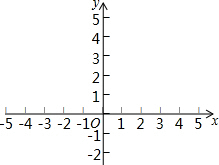问题：探究函数y=|x|-2的图象与性质．小华根据学习函数的经验，对函数y=|x|-2的图象与性质进行了探究．
下面是小华的探究过程，请补充完整：
（1）在函数y=|x|-2中，自变量x可以是任意实数；
（2）如表是y与x的几组对应值．
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 1 | 0 | -1 | -2 | -1 | 0 | m | … |
②若A（n，8），B（10，8）为该函数图象上不同的两点，则n=-10；
（3）如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；
根据函数图象可得：
①该函数的最小值为-2；
②已知直线${y_1}=\frac{1}{2}x-\frac{1}{2}$与函数y=|x|-2的图象交于C、D两点，当y1≥y时x的取值范围是-1≤x≤3．