题目内容
13. 如图,点P为长方形ABCD内一点,连接PA、PB、PC、PD和BD,其中BD、PC交于点Q.若△DPQ和△ABP的面积分别为4.2和20.2,则△BCQ的面积为24.4.
如图,点P为长方形ABCD内一点,连接PA、PB、PC、PD和BD,其中BD、PC交于点Q.若△DPQ和△ABP的面积分别为4.2和20.2,则△BCQ的面积为24.4.
分析 由矩形的性质得出△BCD的面积=$\frac{1}{2}$矩形ABCD的面积,△ABP的面积+△CDP的面积=$\frac{1}{2}$矩形ABCD的面积,得出△BCD的面积=△ABP的面积+△CDP的面积,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴△BCD的面积=$\frac{1}{2}$矩形ABCD的面积,△ABP的面积+△CDP的面积=$\frac{1}{2}$矩形ABCD的面积,
∴△BCD的面积=△ABP的面积+△CDP的面积,
∴△BCQ的面积=△DPQ的面积+△ABP的面积=4.2+20.2=24.4;
故答案为:24.4.
点评 本题考查了矩形的性质、三角形面积的关系;熟练掌握矩形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
3.下列计算正确的是( )
| A. | ($\frac{1}{2}$)2=4 | B. | -52=25 | C. | $\frac{{4}^{2}}{5}$=$\frac{16}{25}$ | D. | -(-$\frac{1}{9}$)2=-$\frac{1}{81}$ |
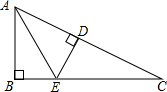 如图,在△ABC中,∠B=90°,E为BC上一点,ED⊥AC于点D,AB=AD,∠C=20°,求∠AEB的度数.
如图,在△ABC中,∠B=90°,E为BC上一点,ED⊥AC于点D,AB=AD,∠C=20°,求∠AEB的度数.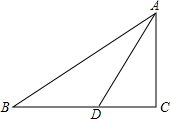 如图,在△ABC中,∠C=90°,AC=5cm,∠BAC的平分线交BC于D,AD=$\frac{10\sqrt{3}}{3}$cm,求∠B,AB,BC.
如图,在△ABC中,∠C=90°,AC=5cm,∠BAC的平分线交BC于D,AD=$\frac{10\sqrt{3}}{3}$cm,求∠B,AB,BC. 如图,已知点D、E、F分别在△ABC的边AB、AC、BC上,DE∥BC、DF∥AC,AE=6,EC=8,求BF:FC的值.
如图,已知点D、E、F分别在△ABC的边AB、AC、BC上,DE∥BC、DF∥AC,AE=6,EC=8,求BF:FC的值.