题目内容
18.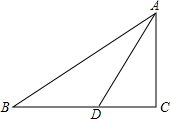 如图,在△ABC中,∠C=90°,AC=5cm,∠BAC的平分线交BC于D,AD=$\frac{10\sqrt{3}}{3}$cm,求∠B,AB,BC.
如图,在△ABC中,∠C=90°,AC=5cm,∠BAC的平分线交BC于D,AD=$\frac{10\sqrt{3}}{3}$cm,求∠B,AB,BC.
分析 在直角三角形ACD中,利用锐角三角函数定义求出cosα的值,确定出α的度数,根据AD为角平分线求出∠BAC的度数,进而求出∠B的度数;利用30度角所对的直角边等于斜边的一半求出AB的长,再利用锐角三角函数定义求出BC的长即可.
解答 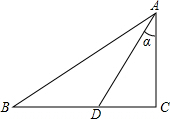 解:∵在△ABC中,∠C=90°,AC=5cm,AD为∠A的平分线,AD=$\frac{10\sqrt{3}}{3}$,
解:∵在△ABC中,∠C=90°,AC=5cm,AD为∠A的平分线,AD=$\frac{10\sqrt{3}}{3}$,
∴cosα=$\frac{5}{\frac{10\sqrt{3}}{3}}$=$\frac{\sqrt{3}}{2}$,
∴α=30°,
∴∠BAC=60°,
∴∠B=90°-60°=30°,
则AB=5×2=10cm,BC=$\frac{5}{tan30°}$=5$\sqrt{3}$cm.
点评 此题属于解直角三角形题型,涉及的知识有:角平分线定义,锐角三角函数定义,特殊角的三角函数值,以及含30度直角三角形的性质,熟练掌握定义及性质是解本题的关键.

练习册系列答案
相关题目
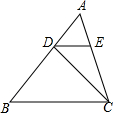 如图,已知:点D、E分别在△ABC的边AB、AC上,DE∥BC,AD:BD:AC=1:2:$\sqrt{3}$,BC=12厘米.
如图,已知:点D、E分别在△ABC的边AB、AC上,DE∥BC,AD:BD:AC=1:2:$\sqrt{3}$,BC=12厘米. 如图,点P为长方形ABCD内一点,连接PA、PB、PC、PD和BD,其中BD、PC交于点Q.若△DPQ和△ABP的面积分别为4.2和20.2,则△BCQ的面积为24.4.
如图,点P为长方形ABCD内一点,连接PA、PB、PC、PD和BD,其中BD、PC交于点Q.若△DPQ和△ABP的面积分别为4.2和20.2,则△BCQ的面积为24.4.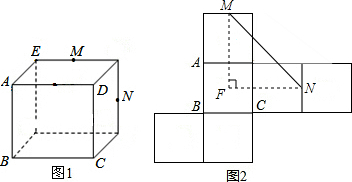
 如图,以AB为直径的圆中,点C为直径AB上任意一点,若分别以AC,BC为直径画半圆,且AB=6cm,求所得两半圆的长度之和.
如图,以AB为直径的圆中,点C为直径AB上任意一点,若分别以AC,BC为直径画半圆,且AB=6cm,求所得两半圆的长度之和.