题目内容
1.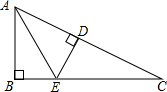 如图,在△ABC中,∠B=90°,E为BC上一点,ED⊥AC于点D,AB=AD,∠C=20°,求∠AEB的度数.
如图,在△ABC中,∠B=90°,E为BC上一点,ED⊥AC于点D,AB=AD,∠C=20°,求∠AEB的度数.
分析 首先在△ABC中,由∠B=90°,∠C=20°,得到∠CAB=70°,再证明Rt△ABE≌Rt△ADE(HL),得到∠BAE=∠DAE,即可求得∠BAE=∠DAE=$\frac{1}{2}∠CAB$=35°,在Rt△ABE中,利用三角形内角和为180°,即可解答.
解答 解:∵在△ABC中,∠B=90°,∠C=20°,
∴∠CAB=70°,
在Rt△ABE和Rt△ADE中,
$\left\{\begin{array}{l}{AB=AD}\\{AE=AE}\end{array}\right.$
∴Rt△ABE≌Rt△ADE(HL),
∴∠BAE=∠DAE,
∴∠BAE=∠DAE=$\frac{1}{2}∠CAB$=35°,
在Rt△ABE中,∠AEB=180°-∠B-∠BAE=180°-90°-35°=55°.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是证明Rt△ABE≌Rt△ADE.

练习册系列答案
相关题目
12.一场足球比赛采用单循环淘汰赛,每队进行5场比赛,每场比赛中胜得3分,和得2分,负得0分,得分最少的会被淘汰,如果其中两队的得分一样,则要计算得失球差来决定胜负.结果北方队和风暴队的成绩最好,同样是3胜、1和、1负,他们各场比赛记录如下:
由以上提供的信息回答下面问题.
(1)两队的得分各是多少?得失球差是多少?
(2)哪个队会被淘汰?
| 队伍/场次 | 1 | 2 | 3 | 4 | 5 |
| 北方队 | 和2:2 | 胜3:1 | 负0:1 | 胜2:1 | 胜3:2 |
| 风暴队 | 胜3:2 | 负0:2 | 胜2:1 | 和2:2 | 和2:2 |
(1)两队的得分各是多少?得失球差是多少?
(2)哪个队会被淘汰?
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①4ac-b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠-1),其中正确的结论有①③④.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①4ac-b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠-1),其中正确的结论有①③④.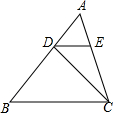 如图,已知:点D、E分别在△ABC的边AB、AC上,DE∥BC,AD:BD:AC=1:2:$\sqrt{3}$,BC=12厘米.
如图,已知:点D、E分别在△ABC的边AB、AC上,DE∥BC,AD:BD:AC=1:2:$\sqrt{3}$,BC=12厘米. 如图,点P为长方形ABCD内一点,连接PA、PB、PC、PD和BD,其中BD、PC交于点Q.若△DPQ和△ABP的面积分别为4.2和20.2,则△BCQ的面积为24.4.
如图,点P为长方形ABCD内一点,连接PA、PB、PC、PD和BD,其中BD、PC交于点Q.若△DPQ和△ABP的面积分别为4.2和20.2,则△BCQ的面积为24.4.