题目内容
1.△ABC中,∠C=90°,若sinA=$\frac{4}{5}$,AB=10,求AC的长.分析 首先由正弦函数的定义可知:$\frac{BC}{AB}=\frac{4}{5}$,而可求得BC的长,然后由勾股定理可求得AC的长.
解答 解:如图所示:
∵sin∠A=$\frac{BC}{AB}=\frac{4}{5}$,AB=10,
∴BC=8,
由勾股定理得:AC=$\sqrt{A{B}^{2}-B{C}^{2}}=\sqrt{1{0}^{2}-{8}^{2}}=6$.
点评 本题主要考查的是解直角三角形,掌握勾股定理和正弦函数的定义是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
12.某种商品进货后,零售价定为每件900元,为了适应市场竞争,商店按零售价的九折降价,并让利40元销售,仍可获利25%,问这种商品的进价为多少元?( )
| A. | 610 | B. | 616 | C. | 648 | D. | 680 |
9.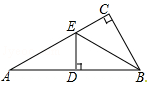 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )
 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
16.△ABC中,∠C=90°,CD⊥AB于D,则sinB=( )
| A. | $\frac{CD}{AB}$ | B. | $\frac{AC}{BC}$ | C. | $\frac{BC}{AB}$ | D. | $\frac{AC}{AB}$ |
6.下列计算结果正确的是( )
| A. | b2•b3=b5 | B. | x3+x3=x6 | C. | (-2x)3=-6x3 | D. | 5a2-3a2=2 |