题目内容
将一副三角板按如图1的位置摆放.
(1)∠1与∠2的关系为 .
(2)在图1中,若EM平分∠BED,EN平分∠FEC,画出图形并求出∠MEN的度数.
(3)在(2)中将图1的45°的三角板绕着直角顶点旋转到图2的位置,其余条件不变,则∠MEN的度数变化吗?若不变,请说明理由;若变化,请求出此时∠MEN的度数.
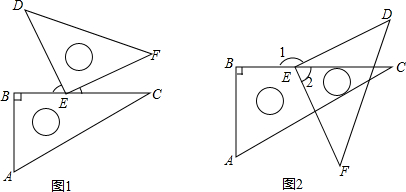
(1)∠1与∠2的关系为
(2)在图1中,若EM平分∠BED,EN平分∠FEC,画出图形并求出∠MEN的度数.
(3)在(2)中将图1的45°的三角板绕着直角顶点旋转到图2的位置,其余条件不变,则∠MEN的度数变化吗?若不变,请说明理由;若变化,请求出此时∠MEN的度数.

考点:角的计算,角平分线的定义
专题:
分析:(1)根据平角的定义及互余的定义解答即可;
(2)根据角平分线的性质解答即可;
(3)根据角平分线的性质解答即可.
(2)根据角平分线的性质解答即可;
(3)根据角平分线的性质解答即可.
解答:解:(1)∵∠1+∠2+∠DEF=180°,∠DEF=90°,
∴∠1+∠2=90°,
故答案为:互余或∠1+∠2=90°;

(2)画出EM和EN,

∵EM平分∠BED,
∴∠MED=
∠BED,
又∵EN平分∠CEF,
∴∠NEF=
∠CEF,
∴∠MEN=∠MED+∠DEF+∠FEN
=
∠BED+90°+
∠CEF
=
(∠BED+∠CEF)+90°
=
×90°+90°
=135°;
(3)不变.
∵EM平分∠BED,
∴∠MED=
∠BED,
又∵EN平分∠CEF,
∴∠NEC=
∠CEF,
∴∠MEN=∠MED+∠DEC+∠CEN
=
∠BED+(∠DEF-∠CEF)+
∠CEF
=
∠BED+(90°-∠CEF)+
∠CEF
=
∠BED+90°-∠CEF+
∠CEF
=
(∠BED-∠CEF)+90°
=
(180°-∠DEC-∠CEF)+90°
=
[180°+90°
=
×90°+90°
=135°.
∴∠1+∠2=90°,
故答案为:互余或∠1+∠2=90°;

(2)画出EM和EN,

∵EM平分∠BED,
∴∠MED=
| 1 |
| 2 |
又∵EN平分∠CEF,
∴∠NEF=
| 1 |
| 2 |
∴∠MEN=∠MED+∠DEF+∠FEN
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=135°;
(3)不变.
∵EM平分∠BED,
∴∠MED=
| 1 |
| 2 |
又∵EN平分∠CEF,
∴∠NEC=
| 1 |
| 2 |
∴∠MEN=∠MED+∠DEC+∠CEN
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=135°.
点评:此题考查了角的计算及角平分线的性质,关键在于认真的观察图形,根据题意找出各个角的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
