题目内容
物价局规定A产品的市场销售单价在15元到40元之间.某商店在销售A产品的过程中发现:销售A产品的成本c(单位:元)与销售件数y(单位:件)成正比例,同时每天的销售件数y与销售价格x(单位:元╱件)之间满足一次函数、二次函数关系中的一种.下表记录了该商店某4天销售A产品的一些数据.
(1)直接写出y与x、c与y之间的函数关系式.
(2)若一天的销售利润w=xy-c
①直接写出每一天的利润w与x之间的函数关系式.
②当销售价格x为多少时,w最大?最大值是多少?
| 销售价格x(单位:元/件) | 15 | 18 | 26 | 34 |
| 销售件数y(单位:件) | 25 | 22 | 14 | 6 |
| 成本c(单位:元) | 300 | 264 | 168 | 72 |
(2)若一天的销售利润w=xy-c
①直接写出每一天的利润w与x之间的函数关系式.
②当销售价格x为多少时,w最大?最大值是多少?
考点:二次函数的应用
专题:
分析:(1)设y与x之间的函数关系式为y=kx+b、c与y之间的函数关系式为c=mx+d,由统计表的数据根据待定系数法求出其解即可.
(2)①由(1)的y、c的解析式代入w=xy-c就可以求出w与x的关系式;
②将①的解析式化为顶点式,由二次函数的性质就可以求出结论.
(2)①由(1)的y、c的解析式代入w=xy-c就可以求出w与x的关系式;
②将①的解析式化为顶点式,由二次函数的性质就可以求出结论.
解答:解:(1)设y与x之间的函数关系式为y=kx+b、c与y之间的函数关系式为c=mx+d,由题意,得
,
,
解得:
,
,
∴y=-x+40,c=-12x+480.
(2)①由题意,得
w=x(-x+40)-(-12x+480),
w=-x2+52x-480.
答:w与x之间的函数关系式为w=-x2+52x-480.
②∵w=-x2+52x-480.
∴w=-(x-26)2+196,
∴a=-1,
∴w有最大值,
∴x=26时,w最大=196.
答:x=26时,w最大=196.
|
|
解得:
|
|
∴y=-x+40,c=-12x+480.
(2)①由题意,得
w=x(-x+40)-(-12x+480),
w=-x2+52x-480.
答:w与x之间的函数关系式为w=-x2+52x-480.
②∵w=-x2+52x-480.
∴w=-(x-26)2+196,
∴a=-1,
∴w有最大值,
∴x=26时,w最大=196.
答:x=26时,w最大=196.
点评:本题考查了待定系数法求一次函数的解析式的运用,二次函数的解析式的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
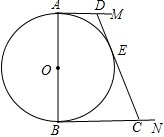 如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM、BN分别交于D、C两点,设AD=x,BC=y,求y关于x的函数解析式,并画出它的图象.
如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM、BN分别交于D、C两点,设AD=x,BC=y,求y关于x的函数解析式,并画出它的图象. 如图,在△ABC中,∠BAC=64°,D、E、F分别为BC、CA、AB上的点,且BD=BF,CD=CE,则∠EDF的度数为
如图,在△ABC中,∠BAC=64°,D、E、F分别为BC、CA、AB上的点,且BD=BF,CD=CE,则∠EDF的度数为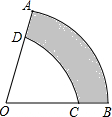 如图所示,
如图所示,
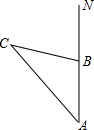 如图,一艘船从港口A处出发,以20海里/时的速度向正北方向航行,该船经过4小时到达B处,港口A北偏西35°方向上有一小岛C,轮船在B处观测到小岛C在北偏西70°的方向上,求从B处到小岛C的距离.
如图,一艘船从港口A处出发,以20海里/时的速度向正北方向航行,该船经过4小时到达B处,港口A北偏西35°方向上有一小岛C,轮船在B处观测到小岛C在北偏西70°的方向上,求从B处到小岛C的距离. 将一副三角板如图所示放在一起,连接AD,则∠ADB的正切值是
将一副三角板如图所示放在一起,连接AD,则∠ADB的正切值是