题目内容
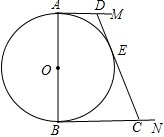 如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM、BN分别交于D、C两点,设AD=x,BC=y,求y关于x的函数解析式,并画出它的图象.
如图,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM、BN分别交于D、C两点,设AD=x,BC=y,求y关于x的函数解析式,并画出它的图象.考点:切线的性质
专题:
分析:作辅助线构造直角三角形,运用勾股定理及切线的性质定理即可求出y关于x的函数解析式;运用描点法作出函数的图象(草图).
解答:解:如图1,过点D作DF⊥BC于点F;

∵AD、BC分别是⊙O的切线,
∴∠OAD=∠OBF=90°,
又∵DF⊥BC,
∴四边形ABFD为矩形,
∴DF=AB=12cm,BF=AD;
∵AD、BC、DC分别为⊙O的切线,
∴DE=DA=x,CE=CB=y,CF=y-x;
∴DC=x+y;
由勾股定理得:DC2=DF2+CF2,
即(x+y)2=(y-x)2+122,
整理得:xy=36,
∴y=
,
∴y关于x的函数解析式y=
(x>0).
如图2,作图象:当x=3时,y=12;x=4时,y=9;x=6时,y=6,x=9时,y=4;
过点A(3,12)、B(4,9)、C(6,6)、D(9,4)
在坐标系内描点连线得函数的图象 (草图)


∵AD、BC分别是⊙O的切线,
∴∠OAD=∠OBF=90°,
又∵DF⊥BC,
∴四边形ABFD为矩形,
∴DF=AB=12cm,BF=AD;
∵AD、BC、DC分别为⊙O的切线,
∴DE=DA=x,CE=CB=y,CF=y-x;
∴DC=x+y;
由勾股定理得:DC2=DF2+CF2,
即(x+y)2=(y-x)2+122,
整理得:xy=36,
∴y=
| 36 |
| x |
∴y关于x的函数解析式y=
| 36 |
| x |
如图2,作图象:当x=3时,y=12;x=4时,y=9;x=6时,y=6,x=9时,y=4;
过点A(3,12)、B(4,9)、C(6,6)、D(9,4)
在坐标系内描点连线得函数的图象 (草图)

点评:该题考查了圆的切线及其性质的应用问题;解题的关键是作辅助线构造直角三角形,运用勾股定理来解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
二次函数y=x2-4x+2与x轴的交点个数是( )
| A、0 | B、1 | C、2 | D、3 |
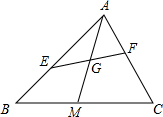 如图,在△ABC中,AM是中线,AB=8,AC=6,E、F分别在AB、AC上,且AE=2AF,EF交AM于点G,则
如图,在△ABC中,AM是中线,AB=8,AC=6,E、F分别在AB、AC上,且AE=2AF,EF交AM于点G,则 如图,AB=m,CD=n,AD⊥BD,BC相交于E,求证:cos∠BED=
如图,AB=m,CD=n,AD⊥BD,BC相交于E,求证:cos∠BED= 如图,在△ABC中,AD平分∠BAC,CE⊥AD,BF⊥AD,求证:
如图,在△ABC中,AD平分∠BAC,CE⊥AD,BF⊥AD,求证: 如图,△ABC中,DE∥BC,
如图,△ABC中,DE∥BC, 如图,Rt△ABC中,斜边AB上一点M,MN⊥AB交AC于N,若AM=3cm,AB:AC=5:4,求MN的长.
如图,Rt△ABC中,斜边AB上一点M,MN⊥AB交AC于N,若AM=3cm,AB:AC=5:4,求MN的长.