题目内容
如图，在△ABC中，∠BAC=64°，D、E、F分别为BC、CA、AB上的点，且BD=BF，CD=CE，则∠EDF的度数为考点：等腰三角形的性质
专题：
分析：图中有两个等腰三角形：△BDF，△CDE．已知∠BAC，根据内角和定理可求∠B+∠C．进而得出∠EDF=180°-∠BDF-∠CDE．
解答：解：∵∠BAC=64°，
∴∠B+∠C=116°，
∵BD=BF，CD=CE，
∴∠BDF=∠BFD，∠CDE=∠CED，
∴∠BDF+∠BFD+∠CDE+∠CED=244°，
即2∠BDF+2∠CDE=244°，
∴∠BDF+∠CDE=122°，
∴∠EDF=180°-（∠BDF+∠CDE）=180°-122°=58°，
故答案为58°．
∴∠B+∠C=116°，
∵BD=BF，CD=CE，
∴∠BDF=∠BFD，∠CDE=∠CED，
∴∠BDF+∠BFD+∠CDE+∠CED=244°，
即2∠BDF+2∠CDE=244°，
∴∠BDF+∠CDE=122°，
∴∠EDF=180°-（∠BDF+∠CDE）=180°-122°=58°，
故答案为58°．
点评：本题考查了等腰三角形的性质：等边对等角．运用三角形内角和定理不难求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
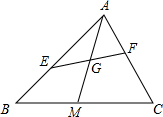如图，在△ABC中，AM是中线，AB=8，AC=6，E、F分别在AB、AC上，且AE=2AF，EF交AM于点G，则
如图，Rt△ABC中，斜边AB上一点M，MN⊥AB交AC于N，若AM=3cm，AB：AC=5：4，求MN的长．
在图中，原点O是△ABC和△A1B1C1的位似中心，△ABC三个顶点坐标分别为A（6，6）、B（8，4）、C（4，0）是点C的对应点，且点C1的横坐标为2．