题目内容
10.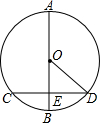 如图,在⊙O中,AB为直径,点B为$\widehat{CD}$的中点,直径AB交弦CD于E,CD=2$\sqrt{5}$,AE=5.
如图,在⊙O中,AB为直径,点B为$\widehat{CD}$的中点,直径AB交弦CD于E,CD=2$\sqrt{5}$,AE=5.(1)求⊙O半径r的值;
(2)点F在直径AB上,连接CF,当∠FCD=∠DOB时,求AF的长.
分析 (1)先根据垂径定理得出E为CD的中点,再由勾股定理即可得出结论;
(2)先由锐角三角函数的定义求出EF的长,再分点F在线段CD的上方与下方两种情况进行讨论即可.
解答 解:(1)∵AB为直径,点B为$\widehat{CD}$的中点,CD=2$\sqrt{5}$,
∴AB⊥CD,
∴DE=$\frac{1}{2}$CD=$\sqrt{5}$.
在Rt△ODE中,
∵OD=r,OE=5-r,DE=$\sqrt{5}$,
∴r2=(5-r)2+($\sqrt{5}$)2,解得r=3;
(2)∵由(1)知,OE=AE-AO=5-3=2,
∴tan∠FCE=tan∠DOB=$\frac{DE}{OE}$=$\frac{\sqrt{5}}{2}$.
在Rt△FCE中,
∵$\frac{EF}{CE}$=$\frac{EF}{\sqrt{5}}$=$\frac{\sqrt{5}}{2}$,
∴EF=$\frac{5}{2}$,
∴当点F在线段CD的上方时,AF=AE-EF=5-$\frac{5}{2}$=$\frac{5}{2}$;
当点F在线段CD的下方时,AF=AE+EF=5+$\frac{5}{2}$=$\frac{15}{2}$>AB,不合题意.
综上所述,AF=$\frac{5}{2}$.
点评 本题考查的是垂径定理,熟知垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
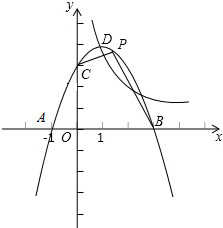 如图,抛物线y=ax2+bx+3与x轴交于A、B两点(A在B的左边),与y轴交于C,tan∠CAB=3;双曲线$y=\frac{k}{x}$(k≠0)经过抛物线y=ax2+bx+3的顶点,点D的横坐标为1.
如图,抛物线y=ax2+bx+3与x轴交于A、B两点(A在B的左边),与y轴交于C,tan∠CAB=3;双曲线$y=\frac{k}{x}$(k≠0)经过抛物线y=ax2+bx+3的顶点,点D的横坐标为1. 如图,在△ABC中,∠C=90°,AB=12,AD是△ABC的一条角平分线.若CD=4,则△ABD的面积为24.
如图,在△ABC中,∠C=90°,AB=12,AD是△ABC的一条角平分线.若CD=4,则△ABD的面积为24.

 利用数轴解下列各题:
利用数轴解下列各题: