题目内容
11.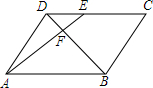 如图,在?ABCD中,点E在CD上,连接AE、BD,且AE、BD交于点F,若EC:DE=4:3,则△DEF与△BAF的周长比是( )
如图,在?ABCD中,点E在CD上,连接AE、BD,且AE、BD交于点F,若EC:DE=4:3,则△DEF与△BAF的周长比是( )| A. | $\frac{4}{3}$ | B. | $\frac{16}{9}$ | C. | $\frac{3}{7}$ | D. | $\frac{7}{3}$ |
分析 根据平行四边形的性质得出AB∥CD,即可得出△DFE∽△BFA,进而利用相似三角形的周长比等于相似比即可得出答案.
解答 解:∵EC:DE=4:3,
∴DE:CD=3:7,
∵在平行四边形ABCD中,
∴AB∥CD,AB=CD,
∴△DFE∽△BFA,
∴$\frac{DE}{AB}=\frac{△DEF的周长}{△BAF的周长}$=$\frac{3}{7}$.
∴△DEF与△BAF的周长比是$\frac{3}{7}$.
故选:C.
点评 此题主要考查了相似三角形的判定与性质以及平行线的性质,根据已知得出△DFE∽△BFA是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.在①4a5b3c2÷(-2a2bc)=abc;②(3.6×10-4)÷4×10-5=9;③$4{x^2}y•(-\frac{1}{2}y)÷4{x^2}{y^2}=-\frac{1}{2}$;④(4xn)2÷xn=8x2n-2中,不正确的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
6.若分式$\frac{|m|-1}{{{m^2}-m}}$的值为零,则m取值为( )
| A. | m=±1 | B. | m=-1 | C. | m=1 | D. | m的值不存在 |
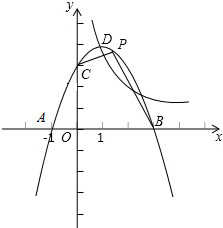 如图,抛物线y=ax2+bx+3与x轴交于A、B两点(A在B的左边),与y轴交于C,tan∠CAB=3;双曲线$y=\frac{k}{x}$(k≠0)经过抛物线y=ax2+bx+3的顶点,点D的横坐标为1.
如图,抛物线y=ax2+bx+3与x轴交于A、B两点(A在B的左边),与y轴交于C,tan∠CAB=3;双曲线$y=\frac{k}{x}$(k≠0)经过抛物线y=ax2+bx+3的顶点,点D的横坐标为1. 利用数轴解下列各题:
利用数轴解下列各题: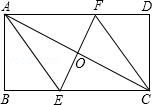 将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,