题目内容
3. 正六边形ABCDEF内接于⊙O,⊙O的半径为2,则$\widehat{AC}$的长为( )
正六边形ABCDEF内接于⊙O,⊙O的半径为2,则$\widehat{AC}$的长为( )| A. | 2π | B. | $\frac{4π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
分析 求出圆心角∠AOC的度数,再利用弧长公式解答即可.
解答 解:如图所示:∵ABCDEF为正六边形,
∴∠AOB=360°×$\frac{1}{6}$=60°,
∴∠AOC=120°,
∴$\widehat{AC}$的长为$\frac{120•π•2}{180}$=$\frac{4}{3}$π.
故选:B.
点评 此题主要考查了正多边形和圆以及弧长计算,此题将扇形的弧长公式与多边形的性质相结合,构思巧妙,利用了正六边形的性质.

练习册系列答案
相关题目
19.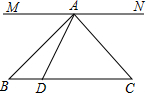 如图,在△ABC中,点D是BC边上一点且CD=CA,过点A作MN∥BC,∠CAN=48°,∠B=41°,∠BAD=( )
如图,在△ABC中,点D是BC边上一点且CD=CA,过点A作MN∥BC,∠CAN=48°,∠B=41°,∠BAD=( )
 如图,在△ABC中,点D是BC边上一点且CD=CA,过点A作MN∥BC,∠CAN=48°,∠B=41°,∠BAD=( )
如图,在△ABC中,点D是BC边上一点且CD=CA,过点A作MN∥BC,∠CAN=48°,∠B=41°,∠BAD=( )| A. | 23° | B. | 24° | C. | 25° | D. | 26° |
8.下列多项式中,能运用公式进行分解因式的是( )
| A. | a2+b2 | B. | m-n2 | C. | x2-9 | D. | x2+2xy-y2. |
12.若代数式$\frac{x+1}{x-3}$有意义,则实数x的取值范围是( )
| A. | x≠-1 | B. | x≥一1且x≠3 | C. | x=3 | D. | x≠3 |
12.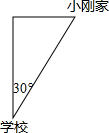 如图所示,小刚家在学校的北偏东30°方向,距离学校2000米,则学校在小刚家的位置是( )
如图所示,小刚家在学校的北偏东30°方向,距离学校2000米,则学校在小刚家的位置是( )
 如图所示,小刚家在学校的北偏东30°方向,距离学校2000米,则学校在小刚家的位置是( )
如图所示,小刚家在学校的北偏东30°方向,距离学校2000米,则学校在小刚家的位置是( )| A. | 北偏东30°,距离小刚家2000米 | B. | 南偏西60°,距离小刚家2000米 | ||
| C. | 南偏西30°,距离小刚家2000米 | D. | 北偏东60°,距离小刚家2000米 |
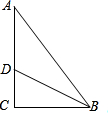 如图,在Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB=5,又△DAB的面积为10,那么DC的长是( )
如图,在Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB=5,又△DAB的面积为10,那么DC的长是( ) 如图,函数y=kx与$y=-\frac{4}{x}$的图象交于点A、B,AC⊥Oy于C,则△ABC的面积为( )
如图,函数y=kx与$y=-\frac{4}{x}$的图象交于点A、B,AC⊥Oy于C,则△ABC的面积为( )