题目内容

19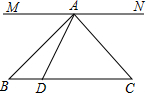．如图，在△ABC中，点D是BC边上一点且CD=CA，过点A作MN∥BC，∠CAN=48°，∠B=41°，∠BAD=（　　）
A．23°B．24°C．25°D．26°

分析 先根据平行线的性质，得出∠C的度数，再根据△ACD是等腰三角形，即可得到∠ADC 的度数，最后根据三角形外角性质即可得到∠BAD的度数．

解答 解：∵MN∥BC，∠CAN=48°，
∴∠C=∠CAN=48°，
∵CD=CA，
∴∠ADC=（180°-48°）÷2=66°，
又∵∠B=41°，∠ADC是△ABD的外角，
∴∠BAD=66°-41°=25°，
故选：C．

点评 本题主要考查了平行线的性质，等腰三角形以及三角形外角性质的运用，解题时注意：两直线平行，内错角相等．

练习册系列答案
相关题目
13．平行四边形具有的性质是（　　）
A．四个角都是90°B．对角线互相垂直C．对角线互相平分D．对角互补
10．已知正方形的面积是18，则它的边长在（　　）
A．5与6之间B．4与5之间C．3与4之间D．2与3之间
7．下列说法不正确的是（　　）
A．一次函数不一定是正比例函数
B．不是一次函数就不一定是正比例函数
C．正比例函数是特殊的一次函数
D．不是正比例函数就一定不是一次函数
14．如图所示，用直尺度量线段AB，可以读出AB的长度为（　　）
A．6cmB．7cmC．8cmD．9cm
3．正六边形ABCDEF内接于⊙O，⊙O的半径为2，则$\widehat{AC}$的长为（　　）
A．2πB．$\frac{4π}{3}$C．$\frac{2π}{3}$D．$\frac{π}{3}$
10．下列能判定AB∥CD的条件有（　　）个．
①∠B+∠BCD=180°；
②∠1=∠2；
③∠3=∠4；
④∠B=∠D．
A．1B．2C．3D．4
7．计算28a4b2÷7a3b的结果是（　　）
A．4ab2B．4a4bC．4a4b2D．4ab
7．某同学带100元钱去买书，已知每册定价8.2元，买书后余下的钱y元和买的册数x之间的函数关系式是（　　）
A．y=8.2xB．y=100-8.2xC．y=8.2x-100D．y=100+8.2x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网