题目内容
16.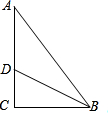 如图,在Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB=5,又△DAB的面积为10,那么DC的长是( )
如图,在Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB=5,又△DAB的面积为10,那么DC的长是( )| A. | 4 | B. | 3 | C. | 5 | D. | 4.5 |
分析 先利用三角形面积求BC的长,最后利用勾股定理可得结论.
解答 解:∵△DAB的面积为10,DA=5,∠C=90°,
∴S△DAB=$\frac{1}{2}$AD•BC=10,
$\frac{1}{2}$×5BC=10,
BC=4,
在Rt△BDC中,由勾股定理得:DC=$\sqrt{B{D}^{2}-B{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
故选B.
点评 本题考查了三角形面积、勾股定理,熟练运用三角形面积公式求边长BC是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图所示,三条直线交于一点,则∠1+∠2+∠3等于( )
如图所示,三条直线交于一点,则∠1+∠2+∠3等于( )
 如图所示,三条直线交于一点,则∠1+∠2+∠3等于( )
如图所示,三条直线交于一点,则∠1+∠2+∠3等于( )| A. | 120° | B. | 150° | C. | 240° | D. | 180° |
13.平行四边形具有的性质是( )
| A. | 四个角都是90° | B. | 对角线互相垂直 | C. | 对角线互相平分 | D. | 对角互补 |
1.下列命题中,是真命题的为( )
| A. | 四个角相等的四边形是矩形 | B. | 四边相等的四边形是正方形 | ||
| C. | 对角线相等的四边形是矩形 | D. | 对角线互相垂直的四边形是菱形 |
8.下列哪个命题是错误的命题( )
| A. | 等边对等角 | |
| B. | 有一个角为60°的等腰三角形为正三角形 | |
| C. | 一个外角等于相邻的两个内角之和 | |
| D. | 到三角形的三边距离相等的点是三角形三条角平分线的交点 |
3.有下列四个命题:①相等的角是对顶角;②两条直线被第三条直线所截,同位角相等;③平行于同一条直线的两条直线互相平行;④垂直于同一条直线的两条直线互相平行.其中真命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3. 正六边形ABCDEF内接于⊙O,⊙O的半径为2,则$\widehat{AC}$的长为( )
正六边形ABCDEF内接于⊙O,⊙O的半径为2,则$\widehat{AC}$的长为( )
 正六边形ABCDEF内接于⊙O,⊙O的半径为2,则$\widehat{AC}$的长为( )
正六边形ABCDEF内接于⊙O,⊙O的半径为2,则$\widehat{AC}$的长为( )| A. | 2π | B. | $\frac{4π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |

