题目内容
 如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°.则线段BC旋转过程中扫过的图形面积为
如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°.则线段BC旋转过程中扫过的图形面积为考点:旋转的性质,扇形面积的计算
专题:
分析:根据网格结构找出点B、C旋转后的对应点B′、C′的位置,先求出AB的长,再根据线段BC旋转过程中扫过的图形面积=扇形ABB′的面积+△AB′C′的面积-△ABC的面积-扇形ACC′的面积,进而计算即可得解.
解答: 解:如图所示:
解:如图所示:
由图可知,AB=
,
所以线段BC旋转过程中扫过的面积
=S扇形AB′B+△AB′C′的面积-△ABC的面积-扇形ACC′的面积
=
-
=
π.
故答案为:
π.
 解:如图所示:
解:如图所示:由图可知,AB=
| 5 |
所以线段BC旋转过程中扫过的面积
=S扇形AB′B+△AB′C′的面积-△ABC的面积-扇形ACC′的面积
=
90π×(
| ||
| 360 |
| 90π×22 |
| 360 |
=
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查了利用旋转变换作图,扇形面积的计算,是基础题,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
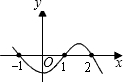 已知y是关于x的函数,函数图象如图,则当y>0时,自变量x的取值范围是( )
已知y是关于x的函数,函数图象如图,则当y>0时,自变量x的取值范围是( )| A、x<0 |
| B、-1<x<1或x>2 |
| C、x>-1 |
| D、x<-1或1<x<2 |
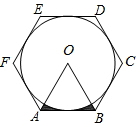 如图,⊙O的外切正六边形ABCDEF的边长为1,则图中阴影部分的面积为( )
如图,⊙O的外切正六边形ABCDEF的边长为1,则图中阴影部分的面积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,AB是⊙O的直径,弦CD平分∠ACB,则∠3=
如图,AB是⊙O的直径,弦CD平分∠ACB,则∠3= 已知反比例函数y=
已知反比例函数y=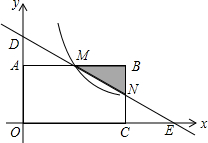 如图在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
如图在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.