题目内容
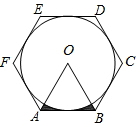 如图,⊙O的外切正六边形ABCDEF的边长为1,则图中阴影部分的面积为( )
如图,⊙O的外切正六边形ABCDEF的边长为1,则图中阴影部分的面积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:正多边形和圆,扇形面积的计算
专题:
分析:由于六边形ABCDEF是正六边形,所以∠AOB=60°,故△OAB是等边三角形,OA=OB=AB=1,设点G为AB与⊙O的切点,连接OG,则OG⊥AB,OG=OA•sin60°,再根据S阴影=S△OAB-S扇形OMN,进而可得出结论.
解答: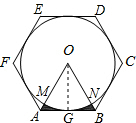 解:∵六边形ABCDEF是正六边形,
解:∵六边形ABCDEF是正六边形,
∴∠AOB=60°,
∴△OAB是等边三角形,OA=OB=AB=1,
设点G为AB与⊙O的切点,连接OG,则OG⊥AB,
∴OG=OA•sin60°=1×
=
,
∴S阴影=S△OAB-S扇形OMN=
×1×
-
=
-
.
故选:A.
 解:∵六边形ABCDEF是正六边形,
解:∵六边形ABCDEF是正六边形,∴∠AOB=60°,
∴△OAB是等边三角形,OA=OB=AB=1,
设点G为AB与⊙O的切点,连接OG,则OG⊥AB,
∴OG=OA•sin60°=1×
| ||
| 2 |
| ||
| 2 |
∴S阴影=S△OAB-S扇形OMN=
| 1 |
| 2 |
| ||
| 2 |
60π×(
| ||||
| 360 |
| ||
| 4 |
| π |
| 8 |
故选:A.
点评:本题考查的是正多边形和圆,根据正六边形的性质求出△OAB是等边三角形是解答此题的关键.

练习册系列答案
相关题目
已知⊙O1的半径r1=2,⊙O2的半径r2是方程
=
的根,当两圆相内切时,⊙O1与⊙O2的圆心距为( )
| 3 |
| x |
| 2 |
| x-1 |
| A、5 | B、4 | C、1或5 | D、1 |
一个两位数,十位数字是x,个位数字是y,如果在它们中间加上一个0得到的数是( )
| A、10x+y |
| B、100x+y |
| C、100y+x |
| D、x+10y |
数轴上的点A表示的数是-1,点B表示的数是-
,则点B关于点A的对称点B′点表示的数为( )
| 2 |
A、
| ||
B、-
| ||
C、-
| ||
| D、0 |
 如图,是由三个相同的小正方体组成的几何体,该几何体的俯视图是( )
如图,是由三个相同的小正方体组成的几何体,该几何体的俯视图是( )A、 |
B、 |
C、 |
D、 |
 如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°.则线段BC旋转过程中扫过的图形面积为
如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°.则线段BC旋转过程中扫过的图形面积为