题目内容
上午8：00，甲船从港口出发，以20海里/时的速度向东行驶，半个小时后，乙船也由同一港口出发，以相同的速度向南航行，上午10：00时，甲乙两船相距多少远？
考点：勾股定理的应用
专题：
分析：根据题意画出图形，利用勾股定理求解即可．
解答：
解：如图所示，
∵甲船从港口出发，以20海里/时的速度向东行驶，
∴OA=20×2=40（海里）．
∵半个小时后，乙船也由同一港口出发，以相同的速度向南航行，
∴OB=20×1.5=30（海里），
∴AB=
=50（海里）．
答：上午10：00时，甲乙两船相距50海里．
解：如图所示，∵甲船从港口出发，以20海里/时的速度向东行驶，
∴OA=20×2=40（海里）．
∵半个小时后，乙船也由同一港口出发，以相同的速度向南航行，
∴OB=20×1.5=30（海里），
∴AB=
| 402+302 |
答：上午10：00时，甲乙两船相距50海里．
点评：本题考查的是勾股定理的应用，根据题意画出图形，利用数形结合求解是解答此题的关键．
练习册系列答案
中考解读考点精练系列答案
相关题目
如图，矩形ABCD中，对角线AC、BD交于点O，AB=6，∠BAC=60°，DE⊥AC交BC于E，则DE的长为（ ）| A、2 | ||
B、4
| ||
C、2
| ||
D、3
|
已知（-2，y1），（-1，y2），（3，y3）是二次函数y=x2-4x+m上的点，则y1，y2，y3的大小关系（ ）
| A、y1＜y2＜y3 |
| B、y2＜y1＜y3 |
| C、y1＜y3＜y2 |
| D、y3＜y2＜y1 |
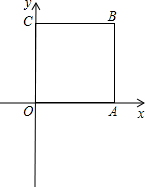如图，四边形OABC为正方形，A（2，0），C（0，2），直线y=3x+m与线段OA、BC相交，且将正方形OABC的面积分成1：2两部分，求m的值．
如图，在四边形ABCD中，对角线AC、BD相交于点O．AB=AD，CB=CD，则图中全等三角形共有（ ）| A、1对 | B、2对 | C、3对 | D、4对 |