题目内容
已知（-2，y1），（-1，y2），（3，y3）是二次函数y=x2-4x+m上的点，则y1，y2，y3的大小关系（ ）
| A、y1＜y2＜y3 |
| B、y2＜y1＜y3 |
| C、y1＜y3＜y2 |
| D、y3＜y2＜y1 |
考点：二次函数图象上点的坐标特征
专题：
分析：先求出抛物线的对称轴，再根据各点到对称轴的距离的大小利用二次函数的增减性求解．
解答：
解：二次函数的对称轴为直线x=-
=2，
∵2-（-2）=4，
2-（-1）=3，
3-2=1，
∴三点到对称轴的距离分别为4、3、1，
又∵a=1＞0，
∴抛物线开口向上，
∴y3＜y2＜y1．
故选D．
| -4 |
| 2×1 |
∵2-（-2）=4，
2-（-1）=3，
3-2=1，
∴三点到对称轴的距离分别为4、3、1，
又∵a=1＞0，
∴抛物线开口向上，
∴y3＜y2＜y1．
故选D．
点评：本题考查了二次函数图象上点的坐标特征，主要利用了二次函数的增减性，求出对称轴解析式并确定出各点到对称轴的距离是解题的关键．
练习册系列答案
相关题目
已知：∠1+∠2=180°，∠3=∠B，AG∥DE，试判断∠G与∠DCB的大小关系，并说明理由．
如图，已知点O是直线AB上的一点，∠DOB=90°，∠COE=90°，图中与∠AOC互补的角有（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
如图，直线AB、CD相交于点O，EO⊥AB于点O，∠EOC=30°，则∠AOD的度数是（ ）| A、60° | B、90° |
| C、120° | D、150° |
已知：如图，AD是△ABC的角平分线，过D点分别作AC和AB的平行线，交AB于点E，交AC于点F．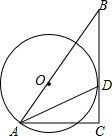
如图，在Rt△ABC中，∠ACB=90°，点O在AB上，⊙O经过点A，且与BC相切于点D