题目内容
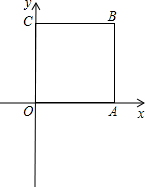 如图,四边形OABC为正方形,A(2,0),C(0,2),直线y=3x+m与线段OA、BC相交,且将正方形OABC的面积分成1:2两部分,求m的值.
如图,四边形OABC为正方形,A(2,0),C(0,2),直线y=3x+m与线段OA、BC相交,且将正方形OABC的面积分成1:2两部分,求m的值.考点:待定系数法求一次函数解析式,正方形的性质
专题:
分析:先根据正方形的性质及直线的性质得到:点D的坐标为:(
,2),点E的坐标为:(-
,0),然后根据正方形的面积及直线y=3x+m与线段OA、BC相交,且将正方形OABC的面积分成1:2两部分,求出一份面积为
,两份面积为
,然后分两种情况讨论:若S四边形OCDE:S四边形ABDE=1:2时,与若S四边形ABDE:S四边形OCDE=1:2时,最后根据梯形的面积公式列出关于m的一元一次方程解答即可.
| 2-m |
| 3 |
| m |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
解答:
解:如图所示,
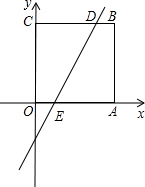
∵四边形OABC为正方形,A(2,0),C(0,2),
∴点D的纵坐标为:2,点E的纵坐标为:0,
∵点D与点E均在直线y=3x+m上,
∴点D的坐标为:(
,2),点E的坐标为:(-
,0),
∵S正方形OABC=2×2=4,且直线y=3x+m将正方形OABC的面积分成1:2两部分,
∴一份面积为
,两份面积为
,
若S四边形OCDE:S四边形ABDE=1:2时,
则S四边形OCDE=
,S四边形ABDE=
,
即:
(OE+CD)•OC=
,
∴
(-
+
)×2=
,
解得:m=-1,
若S四边形ABDE:S四边形OCDE=1:2时,
则S四边形ABDE=
,S四边形OCDE=
,
即:
(OE+CD)•OC=
,
∴
(-
+
)×2=
,
解得:m=-3.
所以m的值为-1或-3.

∵四边形OABC为正方形,A(2,0),C(0,2),
∴点D的纵坐标为:2,点E的纵坐标为:0,
∵点D与点E均在直线y=3x+m上,
∴点D的坐标为:(
| 2-m |
| 3 |
| m |
| 3 |
∵S正方形OABC=2×2=4,且直线y=3x+m将正方形OABC的面积分成1:2两部分,
∴一份面积为
| 4 |
| 3 |
| 8 |
| 3 |
若S四边形OCDE:S四边形ABDE=1:2时,
则S四边形OCDE=
| 4 |
| 3 |
| 8 |
| 3 |
即:
| 1 |
| 2 |
| 4 |
| 3 |
∴
| 1 |
| 2 |
| m |
| 3 |
| 2-m |
| 3 |
| 4 |
| 3 |
解得:m=-1,
若S四边形ABDE:S四边形OCDE=1:2时,
则S四边形ABDE=
| 4 |
| 3 |
| 8 |
| 3 |
即:
| 1 |
| 2 |
| 8 |
| 3 |
∴
| 1 |
| 2 |
| m |
| 3 |
| 2-m |
| 3 |
| 8 |
| 3 |
解得:m=-3.
所以m的值为-1或-3.
点评:本题考查了待定系数法求一次函数解析式,解题的关键是:直线y=3x+m将正方形OABC的面积分成1:2两部分,要分两种情况讨论.

练习册系列答案
相关题目
 如图所示,扳手的开口a的值为2
如图所示,扳手的开口a的值为2| 3 |
| A、2cm | ||||
B、
| ||||
C、
| ||||
| D、1cm |
 如图,直线AB、CD相交于点O,EO⊥AB于点O,∠EOC=30°,则∠AOD的度数是( )
如图,直线AB、CD相交于点O,EO⊥AB于点O,∠EOC=30°,则∠AOD的度数是( )| A、60° | B、90° |
| C、120° | D、150° |
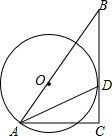 如图,在Rt△ABC中,∠ACB=90°,点O在AB上,⊙O经过点A,且与BC相切于点D
如图,在Rt△ABC中,∠ACB=90°,点O在AB上,⊙O经过点A,且与BC相切于点D 在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂一只白炽灯泡A.为了集中光线,加上了灯罩,如图所示.已知灯罩深8cm,灯泡离地面2m,为了使光线恰好照在墙角,则灯罩的直径应为多少(DE、GF分别为地面与天花板的对角线.计算结果精确到0.01m)?
在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂一只白炽灯泡A.为了集中光线,加上了灯罩,如图所示.已知灯罩深8cm,灯泡离地面2m,为了使光线恰好照在墙角,则灯罩的直径应为多少(DE、GF分别为地面与天花板的对角线.计算结果精确到0.01m)?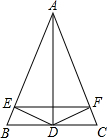 如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F为垂足,则下列四个结论:(1)∠BAD=∠CAD;(2)ED=FD;(3)AD平分∠EDF;(4)AD,EF互相垂直平分.其中正确的有( )
如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F为垂足,则下列四个结论:(1)∠BAD=∠CAD;(2)ED=FD;(3)AD平分∠EDF;(4)AD,EF互相垂直平分.其中正确的有( ) 如图所示,∠DBC=2∠ABD,∠DCB=2∠ACD,若∠BDC=α+
如图所示,∠DBC=2∠ABD,∠DCB=2∠ACD,若∠BDC=α+