题目内容
已知二次函数y=a(x-m)2+n的图象经过(0,5)、(10,8)两点.若a<0,0<m<10,则m的值可能是( )
| A、2 | B、8 | C、3 | D、5 |
考点:二次函数图象上点的坐标特征
专题:
分析:根据二次函数的对称性确定出对称轴的范围,然后求解即可.
解答:
解:∵a<0,
∴抛物线开口向下,
∵图象经过(0,5)、(10,8)两点,0<m<10,
∴对称轴在5到10之间,
∴m的值可能是8.
故选B.
∴抛物线开口向下,
∵图象经过(0,5)、(10,8)两点,0<m<10,
∴对称轴在5到10之间,
∴m的值可能是8.
故选B.
点评:本题考查了二次函数图象上点的坐标特征,从二次函数的对称性考虑求解是解题的关键.

练习册系列答案
相关题目
 如图,已知点O是直线AB上的一点,∠DOB=90°,∠COE=90°,图中与∠AOC互补的角有( )
如图,已知点O是直线AB上的一点,∠DOB=90°,∠COE=90°,图中与∠AOC互补的角有( )| A、1个 | B、2个 | C、3个 | D、4个 |
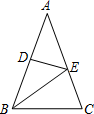 如图,等腰△ABC的周长为16,底边BC=4,AB=AC,∠A=36°,线段AB的垂直平分线交AB于点D,交AC于点E,连接BE.则下列说法中错误的是( )
如图,等腰△ABC的周长为16,底边BC=4,AB=AC,∠A=36°,线段AB的垂直平分线交AB于点D,交AC于点E,连接BE.则下列说法中错误的是( )| A、△CBE是等腰三角形 |
| B、BE平分∠ABC |
| C、△ABE的周长为12 |
| D、△CBE的周长为10 |
 已知如图,OA=OB,OC=OD,∠O=50°,∠C=35°,则∠BED=
已知如图,OA=OB,OC=OD,∠O=50°,∠C=35°,则∠BED= 已知:如图,AD是△ABC的角平分线,过D点分别作AC和AB的平行线,交AB于点E,交AC于点F.
已知:如图,AD是△ABC的角平分线,过D点分别作AC和AB的平行线,交AB于点E,交AC于点F.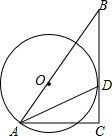 如图,在Rt△ABC中,∠ACB=90°,点O在AB上,⊙O经过点A,且与BC相切于点D
如图,在Rt△ABC中,∠ACB=90°,点O在AB上,⊙O经过点A,且与BC相切于点D