��Ŀ����
17������ABCD�У�AB=12��BC=25��EΪBC��һ�㣨BE��EC����AE��DE��FΪBE��һ�㣬EF=7������AF��GΪED��һ�㣬EG=6����G��GH��ED��BC�ӳ�����H������EGH��ÿ��1����λ���ٶ���EB���B�����ƶ���ͬʱ��P��A���������ÿ��1����λ���ٶ���AD���D�����ƶ������˶��еġ�EGHΪ��E��G��H�䣬��E�䵽���յ�Bʱ����E��G��H�����Pͬʱֹͣ�˶����˶��е�E��G������ֱ����AE�ཻ��Q����AF�ཻ��M����PA=PQʱ��QM=$\frac{35}{9}$������ ��CE=x����BE=25-x����֤����ABE�ס�ECD���ó���Ӧ�߳ɱ������ó�$\frac{25-x}{12}=\frac{12}{x}$���ⷽ�̼������CE��BE�����ݹ��ɶ������AE��ֱ�����������߱ȶ�Ϊ��3��4��5������P��PK��AQ��K����AK=$\frac{4}{5}$t���ɵ��������ε��������AQ��QE����$\frac{5}{4}$QE=EE��ó����̣��ⷽ�����t���ó�EE�䡢E��Q��֤��G��E��=G��F����M��MJ��BC��J�����ݵ��������ε����ߺ�һ���ʵó�E��J=$\frac{1}{2}$E��F=$\frac{2}{3}$�����E��M�����ɵó�QM��
��� �⣺��CE=x����BE=25-x��
���ı���ABCD�Ǿ��Σ�
��CD=AB=12����B=��BCD=90�㣬
���AEB+��BAE=90�㣬
��AE��DE��
���AED=90�㣬
���AEB+��DEC=90�㣬
���BAE=��DEC��
���ABE�ס�ECD��
��$\frac{BE}{CD}=\frac{AB}{CE}$��
��$\frac{25-x}{12}=\frac{12}{x}$��
��ã�x=16����x=9��
��CE��BE��
��CE=9��BE=16��
��AE=$\sqrt{1{2}^{2}+1{6}^{2}}$=20��
��AB��BE��AE=3��4��5��
��Rt��ABE��Rt��ECD��Rt��ADE�����߱ȶ�Ϊ��3��4��5��
����P��PK��AQ��K����ͼ��ʾ��
��AP=t��AK=$\frac{4}{5}$t��
��PA=PQ��
��AK=QK��
��AQ=2AK=$\frac{8}{5}$t��
��QE=20-$\frac{8}{5}$t��
��GG��=HH��=EE��=t��
��$\frac{5}{4}$QE=EE�䣬
��$\frac{5}{4}$��20-$\frac{8}{5}$t��=t��
��ã�t=$\frac{25}{3}$��
��EE��=$\frac{25}{3}$��
��E��Q=$\frac{25}{3}$��$\frac{5}{3}$=5��
��EF=7��
��BF=16-7=9��E��F=EE��-EF=$\frac{25}{3}$-7=$\frac{4}{3}$��
��AF=$\sqrt{{9}^{2}+1{2}^{2}}$=15��
��sin��AFB=$\frac{12}{15}$=$\frac{4}{5}$=sin��QE��E��
���AFB=��QE��E��
��G��E��=G��F��
��M��MJ��BC��J��
��E��J=$\frac{1}{2}$E��F=$\frac{2}{3}$��
��E��M=$\frac{2}{3}$��$\frac{5}{3}$=$\frac{10}{9}$��
��QM=5-$\frac{10}{9}$=$\frac{35}{9}$����
���� �������������ۺ���Ŀ�����������������ε��ж������ʡ����ɶ��������Ǻ��������������ε��ж������ʡ����ε����ʵ�֪ʶ�������ѶȽϴ��ۺ���ǿ����Ҫͨ�����������������Ǻ������ɶ������ܵó������

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�| A�� | $\frac{{a}^{2}-{b}^{2}}{��a-b��^{2}}=\frac{a+b}{a-b}$ | B�� | $\frac{{a}^{2}-{b}^{2}}{{a}^{2}+{b}^{2}}=\frac{a-b}{a+b}$ | ||
| C�� | $\frac{x-1}{1-{x}^{2}}=\frac{1}{x+1}$ | D�� | $\frac{-x-y}{-x+y}=\frac{x-y}{x+y}$ |
| A�� | x2-1 | B�� | x��x-2��+��2-x�� | C�� | x2-2 | D�� | x2-2x+1 |
| A�� | m4-8m2+64=��m2-8��2 | B�� | x4-y4=��x2+y2����x2-y2�� | ||
| C�� | 4a2-4a+1=��2a-1��2 | D�� | a��x-y��-b��y-x��=��x-y����a-b�� |
 ��ͼ����ABC�У�AB=5��BC=3��AC=4���Ե�CΪԲ�ĵ�Բ��AB���У����C�İ뾶Ϊ��������
��ͼ����ABC�У�AB=5��BC=3��AC=4���Ե�CΪԲ�ĵ�Բ��AB���У����C�İ뾶Ϊ��������| A�� | 2.3 | B�� | 2.4 | C�� | 2.5 | D�� | 2.6 |
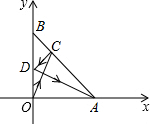 ��ͼ��һ�����ߴӵ�O��������ھ���A��1��0����B��0��1���ľ����ϵĵ�C����AB��������յ�������y��λ�õľ����ϵ�D�㣬���y���ٷ���Ĺ���ǡ�þ�����A�����C������Ϊ��$\frac{1}{3}$��$\frac{2}{3}$����
��ͼ��һ�����ߴӵ�O��������ھ���A��1��0����B��0��1���ľ����ϵĵ�C����AB��������յ�������y��λ�õľ����ϵ�D�㣬���y���ٷ���Ĺ���ǡ�þ�����A�����C������Ϊ��$\frac{1}{3}$��$\frac{2}{3}$����