题目内容
7. 如图,△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( )
如图,△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( )| A. | 2.3 | B. | 2.4 | C. | 2.5 | D. | 2.6 |
分析 首先根据题意作图,由AB是⊙C的切线,即可得CD⊥AB,又由在直角△ABC中,∠C=90°,AC=3,BC=4,根据勾股定理求得AB的长,然后由S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,即可求得以C为圆心与AB相切的圆的半径的长.
解答 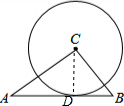 解:在△ABC中,
解:在△ABC中,
∵AB=5,BC=3,AC=4,
∴AC2+BC2=32+42=52=AB2,
∴∠C=90°,
如图:设切点为D,连接CD,
∵AB是⊙C的切线,
∴CD⊥AB,
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
∴AC•BC=AB•CD,
即CD=$\frac{AC•BC}{AB}$=$\frac{3×4}{5}$=$\frac{12}{5}$,
∴⊙C的半径为$\frac{12}{5}$,
故选B.
点评 此题考查了圆的切线的性质,勾股定理,以及直角三角形斜边上的高的求解方法.此题难度不大,解题的关键是注意辅助线的作法与数形结合思想的应用.

练习册系列答案
相关题目
12.若点P1(x1,y1),P2(x2,y2)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,且x1=-x2,则( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | y1=-y2 |
19.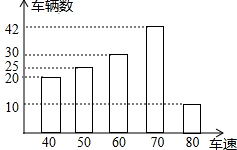 为了了解一路段车辆行驶速度的情况,交警统计了该路段上午7::0至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数、中位数分别是( )
为了了解一路段车辆行驶速度的情况,交警统计了该路段上午7::0至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数、中位数分别是( )
 为了了解一路段车辆行驶速度的情况,交警统计了该路段上午7::0至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数、中位数分别是( )
为了了解一路段车辆行驶速度的情况,交警统计了该路段上午7::0至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数、中位数分别是( )| A. | 众数是80千米/时,中位数是60千米/时 | |
| B. | 众数是70千米/时,中位数是70千米/时 | |
| C. | 众数是60千米/时,中位数是60千米/时 | |
| D. | 众数是70千米/时,中位数是60千米/时 |
 如图,几何体上半部为正三棱柱,下半部为圆柱,其俯视图是( )
如图,几何体上半部为正三棱柱,下半部为圆柱,其俯视图是( )


