题目内容
8.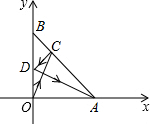 如图,一束光线从点O射出,照在经过A(1,0)、B(0,1)的镜面上的点C,经AB反射后,又照到竖立在y轴位置的镜面上的D点,最后经y轴再反射的光线恰好经过点A,则点C的坐标为($\frac{1}{3}$,$\frac{2}{3}$).
如图,一束光线从点O射出,照在经过A(1,0)、B(0,1)的镜面上的点C,经AB反射后,又照到竖立在y轴位置的镜面上的D点,最后经y轴再反射的光线恰好经过点A,则点C的坐标为($\frac{1}{3}$,$\frac{2}{3}$).
分析 应先作出点O及点A的像,过两个像的直线与直线AB的交点即为所求点.
解答 解:如图所示,
∵点O关于AB的对称点是O′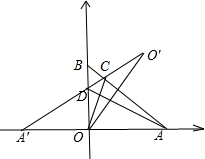 (1,1),
(1,1),
点A关于y轴的对称点是A′(-1,0)
设AB的解析式为y=kx+b,
∵(1,0),(0,1)在直线上,
∴$\left\{\begin{array}{l}{k+b=0}\\{b=1}\end{array}\right.$,解得k=-1,
∴AB的表达式是y=1-x,
同理可得O′A′的表达式是y=$\frac{x}{2}$+$\frac{1}{2}$,
两个表达式联立,解得x=$\frac{1}{3}$,y=$\frac{2}{3}$.
故答案为:($\frac{1}{3}$,$\frac{2}{3}$).
点评 考查镜面对称的知识;根据作相关点的像得到点D的位置是解决本题的关键.

练习册系列答案
相关题目
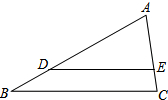 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若$\frac{AE}{AC}$=$\frac{3}{4}$,AD=6,则AB等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若$\frac{AE}{AC}$=$\frac{3}{4}$,AD=6,则AB等于( ) 如图,在边长为80cm的正方形的一个角剪去一个边长为20cm的正方形,则剩下纸片的面积为6000cm2.
如图,在边长为80cm的正方形的一个角剪去一个边长为20cm的正方形,则剩下纸片的面积为6000cm2.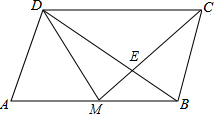 如图,M是?ABCD的边AB的中点,CM与BD相交于点E,求:
如图,M是?ABCD的边AB的中点,CM与BD相交于点E,求: