题目内容
19．
△ABC，D、E分别为AB、AC中点，S△ABC=8，则△DEC的面积为（ ）| A． | 6 | B． | 4 | C． | 2 | D． | 1 |
分析 根据三角形的中位线定义得出DE是△ABC的中位线，再由中位线的性质得出△ADE∽△ABC，根据相似三角形的性质求得△ADE的面积，则△DEC的面积=△ADE的面积．
解答 解：∵△ABC，D、E分别为AB、AC中点，
∴DE是△ABC的中位线，
∴DE∥BC，且DE=$\frac{1}{2}$BC，
∴△ADE∽△ABC，S△DEC=S△ADE，
∴S△ADE=$\frac{1}{4}$S△ABC=2．
∴S△DEC=S△ADE=2．
故选：C．
点评 本题考查了三角形的中位线定理的应用，以及相似三角形的判定和性质，熟记相似三角形的面积的比等于相似比的平方是解题关键．
练习册系列答案
相关题目
9．
由6个小正方体组成了一个几何体（如图所示），如果将标有①的小正方体拿走，那么下列说法正确的是（ ）
由6个小正方体组成了一个几何体（如图所示），如果将标有①的小正方体拿走，那么下列说法正确的是（ ）| A． | 左视图不变，俯视图变化 | B． | 主视图变化，左视图不变 | ||
| C． | 左视图变化，俯视图变化 | D． | 主视图变化，俯视图不变 |
10．实数-$\sqrt{2}$的相反数是（ ）
| A． | -$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | -$\frac{1}{\sqrt{2}}$ | D． | $\frac{1}{\sqrt{2}}$ |
11．若二次根式$\sqrt{x-1}$在实数范围内有意义，则x的取值范围是（ ）
| A． | x≤-1 | B． | x≥-1 | C． | x≤1 | D． | x≥1 |
8．
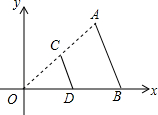如图，线段AB两个端点的坐标分别为A（6，6），B（8，0），以原点O为位似中心，在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD，则端点C的坐标为（ ）
如图，线段AB两个端点的坐标分别为A（6，6），B（8，0），以原点O为位似中心，在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD，则端点C的坐标为（ ）| A． | （3，0） | B． | （4，0） | C． | （3，3） | D． | （4，3） |
如图中的折线ABC表示某汽车的耗油量y（单位：L/km）与速度x（单位：km/h）之间的函数关系（30≤x≤120），已知线段BC表示的函数关系中，该汽车的速度每增加1km/h，耗油量增加0.002L/km．