题目内容
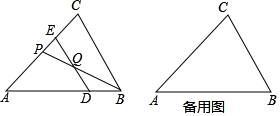
3.在Rt△ABC中,∠ABC=90°,AC=5,BC=3,CD是∠ACB的平分线,将△ABC沿直线CD翻折,点A落在点E处,那么AE的长是2$\sqrt{5}$.分析 由勾股定理求AB=4,再根据旋转的性持和角平分线可知:点A的对应点E在直线CB上,BE=2,利用勾股定理可求AE的长.
解答 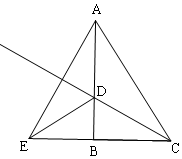 解:∵CD是∠ACB的平分线,
解:∵CD是∠ACB的平分线,
∴将△ABC沿直线CD翻折,点A的对应点E在直线CB上,
∵∠ABC=90°,AC=5,BC=3,
∴AB=4,
由旋转得:EC=AC=5,
∴BE=5-3=2,
在Rt△ABE中,由勾股定理得:AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
故答案为:2$\sqrt{5}$.
点评 本题考查了翻折变换的性质、勾股定理,明确折叠前后的两个角相等,两边相等;在图形中确定直角三角形,如果知道了一个直角三角形的两条边,可以利用勾股定理求第三边.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
13. 如图,正方形ABCD的边长为2,O是边AB上一动点,以O为圆心,2为半径作圆,分别与AD、BC相交于M、N,则扇形OMN的面积S的范围是( )
如图,正方形ABCD的边长为2,O是边AB上一动点,以O为圆心,2为半径作圆,分别与AD、BC相交于M、N,则扇形OMN的面积S的范围是( )
 如图,正方形ABCD的边长为2,O是边AB上一动点,以O为圆心,2为半径作圆,分别与AD、BC相交于M、N,则扇形OMN的面积S的范围是( )
如图,正方形ABCD的边长为2,O是边AB上一动点,以O为圆心,2为半径作圆,分别与AD、BC相交于M、N,则扇形OMN的面积S的范围是( )| A. | $\frac{2}{3}$π≤s≤π | B. | $\frac{1}{2}$π≤s≤π | C. | $\frac{\sqrt{3}}{3}$π≤s≤π | D. | 0≤s≤π |
11.如果一斜坡的坡比是1:2.4,那么该斜坡坡角的余弦值是( )
| A. | $\frac{12}{5}$ | B. | $\frac{5}{12}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
12.抛物线y=2x2+4与y轴的交点坐标是( )
| A. | (0,2) | B. | (0,-2) | C. | (0,4) | D. | (0,-4) |
 如图,已知直线a∥b∥c,直线m交直线a、b、c于点A,B,C,直线n交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,求$\frac{DE}{EF}$的值.
如图,已知直线a∥b∥c,直线m交直线a、b、c于点A,B,C,直线n交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,求$\frac{DE}{EF}$的值.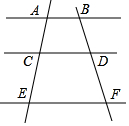 如图,AB∥CD∥EF,如果AC=2,AE=5.5,DF=3,那么BD=$\frac{12}{7}$.
如图,AB∥CD∥EF,如果AC=2,AE=5.5,DF=3,那么BD=$\frac{12}{7}$.