题目内容
18．
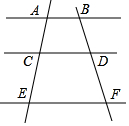如图，AB∥CD∥EF，如果AC=2，AE=5.5，DF=3，那么BD=$\frac{12}{7}$．
分析 根据平行线分线段成比例定理即可得到结论．
解答 解：∵AC=2，AE=5.5，
∴CE=3.5，
AB∥CD∥EF，
∴$\frac{AC}{CE}=\frac{BD}{DF}$，
∴BD=$\frac{12}{7}$，
故答案为：$\frac{12}{7}$．
点评 本题考查平行线分线段成比例定理，用到的知识点是平行线分线段成比例定理，关键是找准对应关系，列出比例式．
练习册系列答案
相关题目
如图，△ABC是等边三角形，点D为AC边上一点，以BD为边作等边△BDE，连接CE，若CD=1，CE=4，则BC=5．
如图，是由6个正方体搭成的几何体，画出从正面、左面、上面看到的形状图．
6．下列运算正确的是（ ）
| A． | 3a+2b=5ab | B． | 5x2y-4x2y=x2y | C． | x2+3x3=4x5 | D． | 5x3-2x3=3 |
13．在△ABC中，点D、E分别在边AB、AC上，联结DE，那么下列条件中不能判断△ADE和△ABC相似的是（ ）
| A． | DE∥BC | B． | ∠AED=∠B | C． | AE：AD=AB：AC | D． | AE：DE=AC：BC |
10．已知非零向量$\vec a$，$\vec b$，$\vec c$，下列条件中，不能判定$\vec a$∥$\vec b$的是 （ ）
| A． | $\vec a$∥$\vec c$，$\vec b$∥$\vec c$ | B． | $|{\overrightarrow a}|=2|{\overrightarrow b}|$ | C． | $\vec a$=$-2\vec b$ | D． | $\vec a$=$2\vec c$，$\vec b$=$\vec c$ |
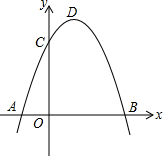如图，抛物线y=-x2+bx+c过点B（3，0），C（0，3），D为抛物线的顶点．