题目内容
13.在△ABC中,如果AB=AC=10,cosB=$\frac{4}{5}$,那么△ABC的重心到底边的距离为2.分析 根据等腰三角形的三线合一,知三角形的重心在BC边的高上.根据勾股定理求得该高,再根据三角形的重心到顶点的距离是它到对边中点的距离的2倍,求得G到BC的距离.
解答 解:∵AB=AC=10,
∴△ABC是等腰三角形
∴三角形的重心G在BC边的高
∵cosB=$\frac{4}{5}$,
∴在BC边的高=6,
根据三角形的重心性质
∴G到BC的距离是2.
故答案为:2
点评 本题考查了三角形的重心,熟记三角形的重心到顶点的距离等于到对边中点的距离的2倍是解题的关键.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
5.已知二次函数y=x2,将它的图象向左平移2个单位,再向上平移3个单位,则所得图象的表达式为( )
| A. | y=(x+2)2+3 | B. | y=(x+2)2-3 | C. | y=(x-2)2+3 | D. | y=(x-2)2-3 |
2.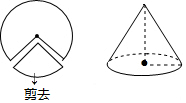 如图,从半径为9cm的圆形纸片中剪去一个扇形,使剪去的扇形的弧长为圆周长的$\frac{1}{3}$,将留下的扇形纸片围成一个圆锥(接缝处不重叠),则这个圆锥的高为( )
如图,从半径为9cm的圆形纸片中剪去一个扇形,使剪去的扇形的弧长为圆周长的$\frac{1}{3}$,将留下的扇形纸片围成一个圆锥(接缝处不重叠),则这个圆锥的高为( )
 如图,从半径为9cm的圆形纸片中剪去一个扇形,使剪去的扇形的弧长为圆周长的$\frac{1}{3}$,将留下的扇形纸片围成一个圆锥(接缝处不重叠),则这个圆锥的高为( )
如图,从半径为9cm的圆形纸片中剪去一个扇形,使剪去的扇形的弧长为圆周长的$\frac{1}{3}$,将留下的扇形纸片围成一个圆锥(接缝处不重叠),则这个圆锥的高为( )| A. | 6cm | B. | 3$\sqrt{5}$cm | C. | 8cm | D. | 5$\sqrt{3}$cm |
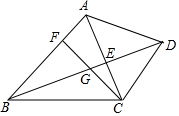 已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GE•GD.
已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GE•GD. 如图,在△ABC中,AB=AC,点D、E是边BC上的两个点,且BD=DE=EC,过点C作CF∥AB交AE延长线于点F,连接FD并延长与AB交于点G;
如图,在△ABC中,AB=AC,点D、E是边BC上的两个点,且BD=DE=EC,过点C作CF∥AB交AE延长线于点F,连接FD并延长与AB交于点G; 已知:如图,在△ABC中,点D,E分别在边AB,BC上,BA•BD=BC•BE
已知:如图,在△ABC中,点D,E分别在边AB,BC上,BA•BD=BC•BE