题目内容
14.类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做等邻边四边形.(1)如图1,四边形ABCD中,AC平分∠BAD,∠B=∠D.求证:四边形ABCD为等邻边四边形.
(2)如图2,Rt△ABC中,∠ABC=90°,AB=2,BC=1,将△ABC沿∠ABC的平分线BB′的方向平移,得到△A′B′C′,连接AA′、BC′,若平移后的四边形ABC′A′是等邻边四边形,且满足BC′=AB,求平移的距离.
(3)如图3,在等邻边四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC和BD为四边形对角线,△BCD为等边三角形,试探究AC和AB的数量关系.

分析 (1)先判断△ABC≌△ADC,得到AB=AD,即可;
(2)根据平移得特征,得到A′B′∥AB,∠A′B′C′=∠ABC=90°,C′B′=CB=1,用勾股定理列出方程求解即可;
(3)先判断出△AED为等边三角形,再说明△BDE≌△CDA,最后用勾股定理即可.
解答 解:(1)∵∠BAC=∠DAC,∠B=∠D,AC=AC,
∴△ABC≌△ADC,
∴AB=AD,
∴四边形ABCD是等邻边四边形.
(2)如图2,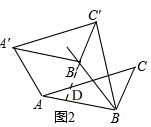 延长C′B′交AB于点D,
延长C′B′交AB于点D,
∵△A′B′C′由△ABC平移得到,
∴A′B′∥AB,∠A′B′C′=∠ABC=90°,C′B′=CB=1,
∴B′D⊥AB,
∵BB′平分∠ABC,
∴∠B′BD=45°,
即B′D=BD
设B′D=BD=x,
∴C′D=1+x,
∵BC′=AB=2,
∴Rt△BDC′中,x2+(1+x)2=4,
解得x1=$\frac{-1+\sqrt{7}}{2}$,x2=$\frac{-1-\sqrt{7}}{2}$(不合题意,舍去),
∴等腰Rt△BB′D中,BB′=$\sqrt{2}$x=$\frac{-\sqrt{2}+\sqrt{14}}{2}$,
∴平移的距离为$\frac{-\sqrt{2}+\sqrt{14}}{2}$,
(3)AC=$\sqrt{2}$AB,
理由:如图3,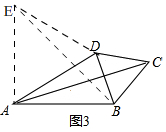 过A作AE⊥AB,且AE=AB,连接ED,EB,
过A作AE⊥AB,且AE=AB,连接ED,EB,
∵AE⊥AB,
∴∠EAD+∠BAD=90°,
又∵∠BAD+∠BCD=90°,△BCD为等边三角形,
∴∠EAD=∠DCB=60°,
∵AE=AB,AB=AD,
∴AE=AD,
∴△AED为等边三角形,
∴AD=ED,∠EDA=∠BDC=60°
∴∠BDE=∠CDA,
∵ED=AD,BD=CD,
∴△BDE≌△CDA,
∴AC=BE
∵AE=BE,∠BAE=90°,
∴BE=$\sqrt{2}$AB,
∴AC=$\sqrt{2}$AB.
点评 此题是几何变换综合题,主要考查新定义等邻边四边形,理解这个新定义,平移得特征,等边三角形的性质,勾股定理,全等三角形的判定和性质,新定义的理解是解本题的关键.

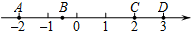 如图,数轴上有A,B,C,D四个点,其中绝对值小于2的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中绝对值小于2的数对应的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
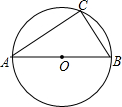 如图,AB为圆O的直径,在圆O上取异于A、B的一点C,并连结BC、AC.过点A作圆O的切线,交直线BC于点D,作∠ADC的角平分线,交AB于点P.若AB=10,BC=6,则AP的长度为(
如图,AB为圆O的直径,在圆O上取异于A、B的一点C,并连结BC、AC.过点A作圆O的切线,交直线BC于点D,作∠ADC的角平分线,交AB于点P.若AB=10,BC=6,则AP的长度为(| A. | 4 | B. | 5 | C. | $\frac{40}{9}$ | D. | $\frac{15}{4}$ |
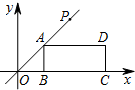 如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(3,3)和点P,且OP=6$\sqrt{2}$.将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )
如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(3,3)和点P,且OP=6$\sqrt{2}$.将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )| A. | 0<b<3 | B. | -3<b<0 | C. | -6<b<-3 | D. | -3<b<3 |
 如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )
如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )| A. | 59° | B. | 31° | C. | 124° | D. | 121° |
 如图,∠A=∠E,AC⊥BE,AB=EF,BE=10,CF=4,则AC=6.
如图,∠A=∠E,AC⊥BE,AB=EF,BE=10,CF=4,则AC=6.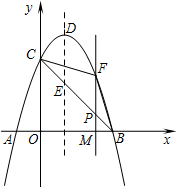 如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.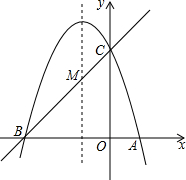 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.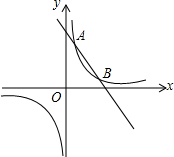 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于点A(2,5)和B,并且点A与点B关于第一、三象限的角平分线对称.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于点A(2,5)和B,并且点A与点B关于第一、三象限的角平分线对称.