题目内容
19.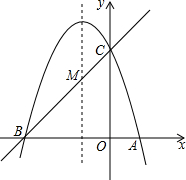 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标.
分析 (1)根据题意得出关于a、b、c的方程组,求得a、b、c的值,即可得出抛物线的解析式,根据抛物线的对称性得出点B的坐标,再设出直线BC的解析式,把点B、C的坐标代入即可得出直线BC的解析式;
(2)点A关于对称轴的对称点为点B,连接BC,设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小,再求得点M的坐标.
解答 解:(1)依题意得:$\left\{\begin{array}{l}{-\frac{b}{2a}=-1}\\{a+b+c=0}\\{c=3}\end{array}\right.$,
解之得:$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$,
∴抛物线解析式为y=-x2-2x+3,
∵对称轴为x=-1,且抛物线经过A(1,0),
∴B(-3,0),
∴把B(-3,0)、C(0,3)分别代入直线y=mx+n,
得$\left\{\begin{array}{l}{-3m+n=0}\\{n=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$,
∴直线y=mx+n的解析式为y=x+3;
(2)设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.
把x=-1代入直线y=x+3得,y=2
∴M(-1,2).
即当点M到点A的距离与到点C的距离之和最小时M的坐标为(-1,2).
点评 本题考查了抛物线与x轴的交点问题,轴对称-最短路线问题,求得抛物线的解析式和直线的解析式是解题的关键.

练习册系列答案
相关题目
7.-$\frac{1}{2016}$的相反数是( )
| A. | $\frac{1}{2016}$ | B. | -$\frac{1}{2016}$ | C. | 2016 | D. | -2016 |
11.下列计算正确的是( )
| A. | x3•x5=x15 | B. | x4÷x=x3 | C. | 3x2•4x2=12x2 | D. | (x5)2=x7 |

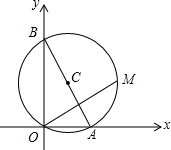 如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为(4$\sqrt{3}$,4).
如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为(4$\sqrt{3}$,4).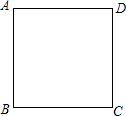 如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°.
如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°.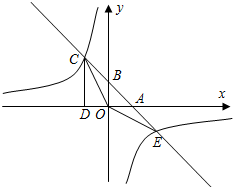 如图,已知一次函数y=k1x+b的图象分别x轴,y轴交于A、B两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OD=1,OE=$\sqrt{10}$,cos∠AOE=$\frac{3\sqrt{10}}{10}$
如图,已知一次函数y=k1x+b的图象分别x轴,y轴交于A、B两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OD=1,OE=$\sqrt{10}$,cos∠AOE=$\frac{3\sqrt{10}}{10}$