题目内容
14.已知∠AOD=α,射线OB、OC在∠AOD的内部,OM平分∠AOC,ON平分∠BOD.(1)如图1,当射线OB与OC重合时,求∠MON的大小;
(2)在(1)的条件下,若射线OC绕点O逆时针旋转一定角度θ,如图2,求∠MON的大小;
(3)在(2)的条件下,射线OC绕点O继续逆时针旋转,旋转到与射线OA的反向延长线重合为止,在这一旋转过程中,∠MON=$\frac{1}{2}$(θ-α).

分析 (1)根据角平分线的定义求出∠BOM和∠BON,然后根据∠MON=∠BOM+∠BON代入数据进行计算即可得解;
(2)根据角平分线的定义求出∠COM和∠BON,然后根据∠MON=∠COM+∠BON-∠BOC代入数据进行计算即可得解;
(3)根据角平分线的定义求出∠AOM=$\frac{1}{2}$∠AOC=90°,∠DON=$\frac{1}{2}$∠BOD,根据∠AOD-∠BOD+BOC=180°求得∠BOD=α+θ-180°,然后根据∠MON=90°-α+$\frac{1}{2}$∠BOD,代入数据进行计算即可得解.
解答 解:(1)∵OM平分∠AOB,ON平分∠BOD,
∴∠BOM=$\frac{1}{2}$∠AOB,∠BON=$\frac{1}{2}$∠BOD,
∴∠MON=∠COM+∠BON-∠BOC=$\frac{1}{2}$(∠AOC+∠BOD),
∵∠AOD=∠AOB+∠BOD=α,
∴∠MON=$\frac{1}{2}$α;
(2)∵OM平分∠AOC,ON平分∠BOD.
∴∠COM=$\frac{1}{2}$∠AOC,∠BON=$\frac{1}{2}$∠BOD,
∴∠MON=∠COM+∠BON-∠BOC=$\frac{1}{2}$(∠AOC+∠BOD)-∠BOC,
∵∠AOD=∠AOC+∠BOD-∠BOC=α,
∴∠AOC+∠BOD=α+θ ,
,
∴∠MON=$\frac{1}{2}$(α+θ)-θ=$\frac{1}{2}$(α-θ);
(3)如图3,∵OM平分∠AOC,ON平分∠BOD.
∴∠AOM=$\frac{1}{2}$∠AOC=90°,∠DON=$\frac{1}{2}$∠BOD,
∴∠MON=90°-α+$\frac{1}{2}$∠BOD,
∵∠AOD-∠BOD+BOC=180°,
∴∠BOD=α+θ-180°,
∴∠MON=90°-α+$\frac{1}{2}$∠BOD=90°-α+$\frac{1}{2}$(α+θ-180°)=$\frac{1}{2}$(θ-α).
故答案为$\frac{1}{2}$(θ-α).
点评 本题考查了角的计算,角平分线的定义,准确识图是解题的关键,难点在于要注意整体思想的利用.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 如图,小将同学将一个直角三角形的纸片折叠,A与B重合,折痕为DE,若已知AC=4,BC=3,∠C=90°,则EC的长为( )
如图,小将同学将一个直角三角形的纸片折叠,A与B重合,折痕为DE,若已知AC=4,BC=3,∠C=90°,则EC的长为( )| A. | $\frac{8}{7}$ | B. | $\frac{7}{8}$ | C. | 2 | D. | $\frac{3}{4}$ |
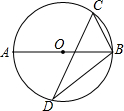 如图,AB为⊙O的直径,∠CDB=30°,则∠CBA=60°.
如图,AB为⊙O的直径,∠CDB=30°,则∠CBA=60°. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).