题目内容

4．某建筑工地在进行勘测时，想用一条60米长的绳子围成一个直角三角形，其中一条边的长度为10米，求这个直角三角形的面积．

分析 首先确定10米长的绳子是直角边，然后设出另一条直角边并表示出斜边，利用勾股定理列出方程求得直角边的长后求得直角三角形的面积即可．

解答 解：因为60÷10=6，所以10米长的边必有一条是直角边，
所以设另一条直角边的长为x米，则斜边长为60-10-x=50-x（米），
由勾股定理得：x2+102=（50-x）2，
解得：x=24，50-x=26，
所以直角三角形的面积为10×24×$\frac{1}{2}$=120平方米．

点评 本题考查了一元二次方程的应用，解题的关键是能够判断出10米长的绳子是直角边还是斜边，从而设出直角三角形的其他变，难度不大．

练习册系列答案
相关题目
14．已知∠AOD=α，射线OB、OC在∠AOD的内部，OM平分∠AOC，ON平分∠BOD．
（1）如图1，当射线OB与OC重合时，求∠MON的大小；
（2）在（1）的条件下，若射线OC绕点O逆时针旋转一定角度θ，如图2，求∠MON的大小；
（3）在（2）的条件下，射线OC绕点O继续逆时针旋转，旋转到与射线OA的反向延长线重合为止，在这一旋转过程中，∠MON=$\frac{1}{2}$（θ-α）．
15．操作：某数学兴趣小组在研究用一副三角板拼角时，小明、小亮分别拼出图1、图2所示的两种图形，如图1，小明把30°和90°的角按如图1方式拼在一起；小亮把30°和90°的角按如图2方式拼在一起，并在各自所拼的图形中分别作出∠AOB、∠COD的平分线OE、OF．小明很容易地计算出图1中∠EOF=60°．

计算：请你计算出图2中∠EOF=75度．
归纳：通过上面的计算猜一猜，当有公共顶点的两个角∠α、∠β有一条边重合，且这两个角在公共边的异侧时，则这两个角的平分线所夹的角=$\frac{1}{2}∠α+\frac{1}{2}∠β$．（用含α、β的代数式表示）
拓展：小明把图1中的三角板AOB绕点O顺时针旋转90°后得到图3，小亮把图2中的三角板AOB绕点O顺时针旋转90°后得到图4（两图中的点O、B、D在同一条直线上）．在图3中，易得到∠EOF=∠DOF-∠BOE=$\frac{1}{2}$∠COD-$\frac{1}{2}$∠AOB=45°-15°=30°；仿照图3的作法，请你通过计算，求出图4中∠EOF的度数（写出解答过程）．
反思：通过上面的拓展猜一猜，当有公共顶点的两个角∠α、∠β（∠α＞∠β）有一条边重合，且这两个角在公共边的同侧时，则这两个角的平分线所夹的角=$\frac{1}{2}∠α-\frac{1}{2}∠β$．
12．如图，CP、BP分别平分△ABC的外角∠ECB，∠DBC，若∠A=50°，那么∠P=65°．
19．在△ABC中，若|sinA-$\frac{1}{2}$|+（$\frac{\sqrt{2}}{2}$-cosB）2=0，则∠C的度数是（　　）
A．45°B．75°C．105°D．120°
9．以下四家银行的图标，是中心对称图形的是（　　）
A．B．C．D．
16．如图所示，在△ABC中，AB=AC，∠A=36°，BD、CE分别为∠ABC与∠ACB的角平分线且相交于点F，则图中的等腰三角形有（　　）
A．6个B．7个C．8个D．9个
13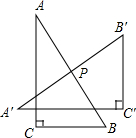．如图，将Rt△ABC绕斜边AB的中点P旋转到△A′B′C′的位置，使得A′C′∥BC，则旋转角等于（　　）
A．60°B．80°C．90°D．100°
14．如图，点A，D，C，F在同一条直线上，且∠B=∠E=90°，添加下列所给的条件后，仍不能判定△ABC与△DEF全等的是（　　）
A．AB=DE，BC=EFB．AC=DF，∠BCA=∠FC．∠A=∠EDF，∠BCA=∠FD．AC=DF，BC=EF

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网