题目内容
3.计算:(1)$\sqrt{16}+(-12)×\root{3}{\frac{1}{8}}-\sqrt{(-1)^{2}}$
(2)$\frac{2+\sqrt{2}}{\sqrt{2}}+\sqrt{18}-4\sqrt{\frac{1}{2}}$
(3)解方程组:$\left\{\begin{array}{l}{2x+y=4}\\{2y+1=5x}\end{array}\right.$
(4)解方程组:$\left\{\begin{array}{l}{\frac{x}{2}-\frac{x-y}{3}=6}\\{x-3y=6}\end{array}\right.$.
分析 (1)原式利用平方根及立方根定义化简,计算即可得到结果;
(2)原式利用二次根式性质化简,计算即可得到结果;
(3)方程组利用代入消元法求出解即可;
(4)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)原式=4-6-1=-3;
(2)原式=$\sqrt{2}$+1+3$\sqrt{2}$-2$\sqrt{2}$=2$\sqrt{2}$+1;
(3)方程组整理得:$\left\{\begin{array}{l}{y=-2x+4①}\\{2y+1=5x②}\end{array}\right.$,
①代入②可得:8-4x+1=5x,
解得:x=1,
把x=1代入①得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$;
(4)方程组整理得:$\left\{\begin{array}{l}{x+2y=36①}\\{x-3y=6②}\end{array}\right.$,
①-②得:5y=30,
解得:y=6,
把y=6代入②得:x=24,
则方程组的解为$\left\{\begin{array}{l}{x=24}\\{y=6}\end{array}\right.$.
点评 此题考查了实数的运算,以及解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.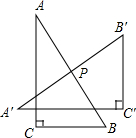 如图,将Rt△ABC绕斜边AB的中点P旋转到△A′B′C′的位置,使得A′C′∥BC,则旋转角等于( )
如图,将Rt△ABC绕斜边AB的中点P旋转到△A′B′C′的位置,使得A′C′∥BC,则旋转角等于( )
 如图,将Rt△ABC绕斜边AB的中点P旋转到△A′B′C′的位置,使得A′C′∥BC,则旋转角等于( )
如图,将Rt△ABC绕斜边AB的中点P旋转到△A′B′C′的位置,使得A′C′∥BC,则旋转角等于( )| A. | 60° | B. | 80° | C. | 90° | D. | 100° |

 如图,AO⊥CO,DO⊥BO.若∠DOC=30°,则∠AOB的度数为150°.
如图,AO⊥CO,DO⊥BO.若∠DOC=30°,则∠AOB的度数为150°.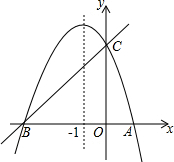 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,求抛物线经过A(1,0),C(0,3)两点,与x轴交于A、B两点.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,求抛物线经过A(1,0),C(0,3)两点,与x轴交于A、B两点.
 如图,CP、BP分别平分△ABC的外角∠ECB,∠DBC,若∠A=50°,那么∠P=65°.
如图,CP、BP分别平分△ABC的外角∠ECB,∠DBC,若∠A=50°,那么∠P=65°.