题目内容
19.计算:tan60°+|$\sqrt{3}$-2|-($\sqrt{7}$-1)0-($\frac{1}{3}$)-1.分析 原式利用特殊角的三角函数值,绝对值的代数意义,零指数幂、负整数指数幂法则计算即可得到结果.
解答 解:原式=$\sqrt{3}$+2-$\sqrt{3}$-1-3=-2.
点评 此题考查了实数的运算,零指数幂、负整数指数幂,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.一个不透明的盒子中装有3个红球,2个白球,这些球除颜色外,没有任何其他区别,从这个盒子中同时随机摸出两个球,所有的可能性如下表:
摸到两个红球的概率为( )
| 红球1 | 红球2 | 红球3 | 白球1 | 白球2 | |
| 红球1 | (红1,红2) | (红1,红3) | (红1,白1) | (红1,白2) | |
| 红球2 | (红2,红3) | (红2,白1) | (红2,白2) | ||
| 红球3 | (红3,白1) | (红3,白2) | |||
| 白球1 | (白1,白2) | ||||
| 白球2 |
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
4.在某次数学竞赛中,某校表现突出,成绩均不低于60分.为了更好地了解某校的成绩分布情况,随机抽取利了其中50名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,结果如表:按规定,成绩在80分以上(包括80分)的选手进入决赛.根据所给信息,请估计该校参赛选手入选决赛的概率为0.3.
| 成绩 | 频率 |
| 60≤x<70 | 0.3 |
| 70≤x<80 | 0.4 |
| 80≤x<90 | 0.2 |
| 90≤x≤100 | 0.1 |
11.甲、乙、丙、丁四名跳高运动员最近10次训练成绩的平均数与方差如下表所示:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择的是( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数/cm | 180 | 180 | 185 | 185 |
| 方差 | 8.2 | 3.9 | 7.5 | 3.9 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
8.下列运算正确的是( )
| A. | 3a+2b=5ab | B. | a3•a2=a6 | C. | a3÷a3=1 | D. | (3a)2=3a2 |
9.下列运算正确的是( )
| A. | (x3)2=x5 | B. | (-x)5=-x5 | C. | x3•x2=x6 | D. | 3x2+2x3=5x5 |
 如图,已知点A的坐标为(5,0),直线y=x+b(b≥0)与y轴交于点B,连接AB,∠α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.
如图,已知点A的坐标为(5,0),直线y=x+b(b≥0)与y轴交于点B,连接AB,∠α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.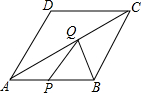 如图,菱形ABCD中,AB=2,∠ADC=120°,P、Q分别是线段AB、AC上的动点,则PQ+BQ的最小值为$\sqrt{3}$.
如图,菱形ABCD中,AB=2,∠ADC=120°,P、Q分别是线段AB、AC上的动点,则PQ+BQ的最小值为$\sqrt{3}$.