题目内容
7.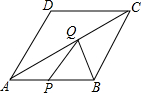 如图,菱形ABCD中,AB=2,∠ADC=120°,P、Q分别是线段AB、AC上的动点,则PQ+BQ的最小值为$\sqrt{3}$.
如图,菱形ABCD中,AB=2,∠ADC=120°,P、Q分别是线段AB、AC上的动点,则PQ+BQ的最小值为$\sqrt{3}$.
分析 过点P作关于AC对称点P′,连接BP'交AC于点Q',由菱形的轴对称性质可知点P'在AD上,然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知BP′⊥AD时BP′=BQ′+PQ′的值最小,然后求解即可.
解答 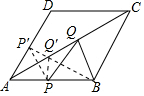 解:
解:
过点P作关于AC对称点P′,连接BP'交AC于点Q,
∵四边形ABCD是菱形,AC为对角线,
∴点P'在AD上,
∵P'Q'=PQ',
∴PQ'+BQ'=BQ′+PQ′=BP',
∵直线外一点到直线的所有连线中垂直线段最短,
∴BP′⊥AD,
∵∠ADC=120°,
∴∠DAC=60°,
∴∠ABP′=30°
∵AB=2,
∴AP′=1,
∴BP′=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查了菱形的性质,轴对称确定最短路线问题,熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
12.下列运算中,正确的是( )
| A. | x2+x3=x5 | B. | (x3)4=x7 | C. | x6÷x2=x3 | D. | 3x2-x2=2x2 |
17.下面调查方式中,合适的是( )
| A. | 调查你所在班级同学的身高,采用抽样调查方式 | |
| B. | 调查湘江的水质情况,采用抽样调查的方式 | |
| C. | 调查CCTV-5《NBA 总决赛》栏目在我市的收视率,采用普查的方式 | |
| D. | 要了解全市初中学生的业余爱好,采用普查的方式 |
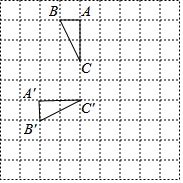 如图,在边长为1的小正方形网格中,将△ABC绕某点旋转到△A'B'C'的位置,则点B运动的最短路径长为$\frac{\sqrt{13}}{2}$π.
如图,在边长为1的小正方形网格中,将△ABC绕某点旋转到△A'B'C'的位置,则点B运动的最短路径长为$\frac{\sqrt{13}}{2}$π.


