题目内容
12.某数学小组的10位同学站成一列做报数游戏,规则是:从前面第一位同学开始,每位同学依次报自己顺序数的倒数的2倍加1,第1位同学报($\frac{2}{1}$+1),第2位同学报($\frac{2}{2}$+1),第3位同学报($\frac{2}{3}$+1)…这样得到的n个数的积为$\frac{1}{2}$(n+1)(n+2).分析 观察不难发现,所报的数的分数部分是分子为2,分母是连续正整数,然后都加上1,把各位同学报的数都化为假分数,即第1位同学报的数是$\frac{3}{1}$,第2位同学报的数是$\frac{4}{2}$,第3位同学报的数是$\frac{5}{3}$,以此类推,得出第n位同学报的数是$\frac{n+2}{n}$,然后根据有理数的乘法运算进行计算即可得解.
解答 解:第1位同学报的数是:$\frac{2}{1}$+1=$\frac{3}{1}$,
第2位同学报的数是:$\frac{2}{2}$+1=$\frac{4}{2}$,
第3位同学报的数是:$\frac{2}{3}$+1=$\frac{5}{3}$,
…,
第n位同学报的数是:$\frac{2}{n}$+1=$\frac{n+2}{n}$,
所以,这样得到的n个数的积为:
$\frac{3}{1}$×$\frac{4}{2}$×$\frac{5}{3}$×…×$\frac{n+2}{n}$=$\frac{1}{2}$(n+1)(n+2).
故答案为$\frac{1}{2}$(n+1)(n+2).
点评 本题考查了规律型:数字的变化类以及倒数的意义,根据题目信息,把各位同学所报的数化为假分数进而得出第n位同学报的数是$\frac{n+2}{n}$是解题的关键.

练习册系列答案
相关题目
2.如果把分式$\frac{2x}{{x}^{2}+{y}^{2}}$中的x和y都扩大3倍,那么分式的值( )
| A. | 扩大3倍 | B. | 不变 | C. | 缩小6倍 | D. | 缩小3倍 |
 抛物线C1:y=a(x+1)(x-3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3)
抛物线C1:y=a(x+1)(x-3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3)
 如图所示,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
如图所示,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( ) 如图,在扇形AOB中,∠AOB=90°,$\widehat{AC}$=$\widehat{BC}$,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为2π-4.
如图,在扇形AOB中,∠AOB=90°,$\widehat{AC}$=$\widehat{BC}$,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为2π-4.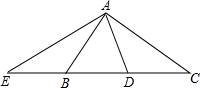 如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,AE⊥AD,交CB的延长线于点E.若AB=1,AC=2,则AE=$\frac{2\sqrt{5}}{3}$.
如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,AE⊥AD,交CB的延长线于点E.若AB=1,AC=2,则AE=$\frac{2\sqrt{5}}{3}$.