题目内容
4. 如图所示,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
如图所示,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )| A. | 45° | B. | 55° | C. | 60° | D. | 65° |
分析 根据内角和定理求得∠BAC=95°,由中垂线性质知DA=DC,即∠DAC=∠C=30°,从而得出答案.
解答 解:在△ABC中,∵∠B=55°,∠C=30°,
∴∠BAC=180°-∠B-∠C=95°,
由作图可知MN为AC的中垂线,
∴DA=DC,
∴∠DAC=∠C=30°,
∴∠BAD=∠BAC-∠DAC=65°,
故选:D.
点评 本题主要考查作图-基本作图,熟练掌握中垂线的作图和性质是解题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
15.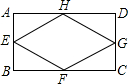 如图所示,在矩形ABCD中,E,F,G,H分别为边AB,BC,CD,DA的中点,若AB=2cm,AD=4cm,则四边形EFGH的面积为( )
如图所示,在矩形ABCD中,E,F,G,H分别为边AB,BC,CD,DA的中点,若AB=2cm,AD=4cm,则四边形EFGH的面积为( )
 如图所示,在矩形ABCD中,E,F,G,H分别为边AB,BC,CD,DA的中点,若AB=2cm,AD=4cm,则四边形EFGH的面积为( )
如图所示,在矩形ABCD中,E,F,G,H分别为边AB,BC,CD,DA的中点,若AB=2cm,AD=4cm,则四边形EFGH的面积为( )| A. | 2cm2 | B. | 4cm2 | C. | 6cm2 | D. | 8cm2 |

 如图,平面直角坐标系中,AB=CD,OA=OC,且OB=3,则D点坐标是(-3,0).
如图,平面直角坐标系中,AB=CD,OA=OC,且OB=3,则D点坐标是(-3,0).