题目内容
2. 如图,在平行四边形ABCD中,E为AD的中点,BE、CD的延长线相交于点F.若△DEF的面积为1,则平行四边形ABCD的面积等于4.
如图,在平行四边形ABCD中,E为AD的中点,BE、CD的延长线相交于点F.若△DEF的面积为1,则平行四边形ABCD的面积等于4.
分析 通过△ABE≌△DFE求得△ABE的面积为1,通过△FBC∽△FED,求得四边形BCDE的面积为3,然后根据?ABCD的面积=四边形BCDE的面积+△ABE的面积即可求得.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,
∵AB∥CD,
∴∠A=∠EDF,
在△ABE和△DFE中,$\left\{\begin{array}{l}{∠A=∠FDE}&{\;}\\{AE=DE}&{\;}\\{∠AEB=∠DEF}&{\;}\end{array}\right.$,
∴△ABE≌△DFE(ASA),
∵△DEF的面积为1,
∴△ABE的面积为1,
∵AD∥BC,
∴△FBC∽△FED,
∴$\frac{{S}_{△EFD}}{{S}_{△BCF}}$=($\frac{ED}{BC}$)2
∵AE=ED=$\frac{1}{2}$AD.
∴ED=$\frac{1}{2}$BC,
∴∴$\frac{{S}_{△EFD}}{{S}_{△BCF}}$=$\frac{1}{4}$,
∴四边形BCDE的面积为3,
∴?ABCD的面积=四边形BCDE的面积+△ABE的面积=4.
故答案为4.
点评 本题考查了平行四边形的性质,三角形全等的判定和性质,三角形相似的判定和性质,熟练掌握三角形全等的性质和三角形相似的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列说法正确的是( )
| A. | 同位角相等 | |
| B. | 和已知直线平行的直线有且只有一条 | |
| C. | 在平面内过一点有且只有一条直线垂直于已知直线 | |
| D. | 在平面内过一点有且只有一条直线平行于已知直线 |
11.已知四边形ABCD为任意凸四边形,E、F、G、H分别是边AB、BC、CD、DA的中点,用S、P分别表示四边形ABCD的面积和周长;S1、P1分别表示四边形EFGH的面积和周长.设K=$\frac{S}{{S}_{1}}$,K1=$\frac{P}{{P}_{1}}$,则下面关于K、K1的说法正确的是( )
| A. | K、K1均为常值 | B. | K为常值,K1不为常值 | ||
| C. | K不为常值,K1为常值 | D. | K、K1均不为常值 |
12. 如图,在平行四边形ABCD中,若E为CD中点,且AE与BD交于点F,则△EDF与△ABF的面积比为( )
如图,在平行四边形ABCD中,若E为CD中点,且AE与BD交于点F,则△EDF与△ABF的面积比为( )
 如图,在平行四边形ABCD中,若E为CD中点,且AE与BD交于点F,则△EDF与△ABF的面积比为( )
如图,在平行四边形ABCD中,若E为CD中点,且AE与BD交于点F,则△EDF与△ABF的面积比为( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:9 |
 的顶点都是正方形网格中的格点,则
的顶点都是正方形网格中的格点,则  等于( )
等于( ) 
 B.
B.  C.
C.  D.
D. 
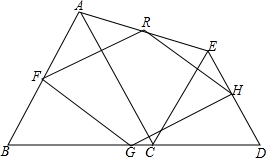 如图,点C是线段BD上的一点,△ABC和△CDE为等边三角形,点F、G、H、R分别为四边形ABDE各边的中点.
如图,点C是线段BD上的一点,△ABC和△CDE为等边三角形,点F、G、H、R分别为四边形ABDE各边的中点.