Question

17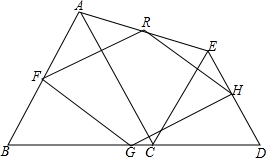．如图，点C是线段BD上的一点，△ABC和△CDE为等边三角形，点F、G、H、R分别为四边形ABDE各边的中点．
（1）求证：四边形FGHR为菱形；
（2）若AB=8，CD=6，求FR的长．

Answer 1

分析 （1）连接AD与B C，首先证得△BCE≌△ACD，即可得到AD=BE，然后利用三角形的中位线定理证得四边形RFGH的四边相等；从而证得四边形RFGH是菱形；
（2）作EN⊥CD于N，根据勾股定理求出BE的长，根据三角形中位线定理解答即可．

解答 解：（1）连接AD、BE，
∵△ABC和△ECD是等边三角形，
∴BC=AC，EC=CD，∠ACB=∠ECD=60°，
∴∠BCE=∠ACD=120°，
在△BCE与△ACD中，
$\left\{\begin{array}{l}{AC=BC}\\{∠BCE=∠ACD}\\{EC=DC}\end{array}\right.$，
∴△BCE≌△ACD（SAS），
∴AD=BE，
∵H、R是AE、AB的中点，
∴HR是△ABE的中位线，即HR=$\frac{1}{2}$BE，
同理可证得：RF=$\frac{1}{2}$AD，FG=$\frac{1}{2}$BE，HG=$\frac{1}{2}$AD，
∴HR=RF=FG=GH，
∴四边形RFGH是菱形；
（2）作EN⊥CD于N，
则CN=$\frac{1}{2}$CD=3，EN=3$\sqrt{3}$，
在Rt△EBN中，BE=$\sqrt{B{N}^{2}+E{N}^{2}}$=2$\sqrt{37}$，
则FR=$\frac{1}{2}$BE=$\sqrt{37}$．

点评 本题考查的是中点四边形的性质，掌握全等三角形的判定定理和性质定理、三角形的中位线定理是解题的关键．