题目内容
13．分解因式：x2-y2-2x-4y-3．分析 先拆项得出x2-2x+1-y2-4y-4，再分组，用完全平方公式分解，最后用平方差公式分解即可．
解答 解：x2-y2-2x-4y-3
=（x2-2x+1）-（y2+4y+4）
=（x-1）2-（u+2）2
=[（x-1）+（y+2）][（x-1）-（y+2）]
=（x+y+1）（x-y-3）．
点评 本题考查了分解因式的应用，能正确分组是解此题的关键，题目比较典型，难度不大．
练习册系列答案
相关题目
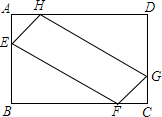如图，在矩形ABCD中，AB=6，BC=8，点E、F、G、H分别在边AB、BC、CD、AD上，且AE=AH=CF=CG，设AE的长为x，四边形EFGH的面积为S．
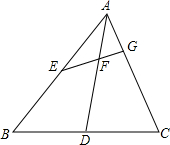在△ABC中，D、E分别为BC、AB的中点，EG⊥AC于点G，EG、AD交于点F，若AG=4，BC=2$\sqrt{29}$，tan∠DAC=$\frac{1}{2}$，则AC=12．
2．下列方程中，解是x=-2的方程是（ ）
| A． | -2x-1=-5 | B． | 3（x-1）-2=11 | C． | -$\frac{1}{2}$x+1=0 | D． | $\frac{x-1}{3}$+1=0 |