题目内容
6.我们知道:$\frac{1}{2}$×$\frac{2}{3}$=$\frac{1}{3}$,$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$=$\frac{1}{4}$,$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×$\frac{4}{5}$=$\frac{1}{5}$,…,$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{n}{n+1}$=$\frac{1}{n+1}$试根据上面的规律,解答下面两题:
(1)计算:($\frac{1}{2}$-1)($\frac{1}{3}$-1)($\frac{1}{4}$-1)…($\frac{1}{100}$-1);
(2)将2016减去它的$\frac{1}{2}$,再减去余下的$\frac{1}{3}$,再减去余下的$\frac{1}{4}$,再减去余下的$\frac{1}{5}$,…依此类推,直到最后减去余下的$\frac{1}{2016}$,最后的结果是多少?
分析 (1)原式括号中变形计算后,约分即可得到结果;
(2)根据题意列出算式,计算即可得到结果.
解答 解:(1)原式=-(1-$\frac{1}{2}$)(1-$\frac{1}{3}$)(1-$\frac{1}{4}$)…(1-$\frac{1}{100}$)=-$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{99}{100}$=-$\frac{1}{100}$;
(2)根据题意得:2006×(1-$\frac{1}{2}$)×(1-$\frac{1}{3}$)×…×(1-$\frac{1}{2006}$)=2006×$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{2005}{2006}$=1.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.下列运用等式的性质变形不正确的是( )
| A. | 若a-b=0,则a=b | B. | 若-$\frac{1}{2}$x=-4,则x=2 | ||
| C. | 若a=b,则2a-5=2b-5 | D. | 若a=b,则$\frac{a}{-4}$=$\frac{b}{-4}$ |
16.下列各题中的变形,属于移项的是( )
| A. | 由2x-2y-1得-1-2y+2x | B. | 由6x-1=x+5得6x-1=5+x | ||
| C. | 由4-x=3x-2得3x-2=4-x | D. | 由2-x=x-2得2+2=x+x |
 如图,已知△ABC内接于⊙O.半径为R,∠A为锐角.求证:$\frac{BC}{sinA}$=2R.
如图,已知△ABC内接于⊙O.半径为R,∠A为锐角.求证:$\frac{BC}{sinA}$=2R.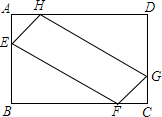 如图,在矩形ABCD中,AB=6,BC=8,点E、F、G、H分别在边AB、BC、CD、AD上,且AE=AH=CF=CG,设AE的长为x,四边形EFGH的面积为S.
如图,在矩形ABCD中,AB=6,BC=8,点E、F、G、H分别在边AB、BC、CD、AD上,且AE=AH=CF=CG,设AE的长为x,四边形EFGH的面积为S.