题目内容
11.解方程:(1)6x+2=5x-7;
(2)2t-5=8t+15;
(3)$\frac{1}{3}$-2y=$\frac{1}{2}$;
(4)4-$\frac{5}{3}$m=-m;
(5)3x+2=5x-7;
(6)-4x+1=$\frac{1}{4}$x.
分析 (1)方程移项合并,把x系数化为1,即可求出解;
(2)方程移项合并,把t系数化为1,即可求出解;
(3)方程去分母,移项合并,把y系数化为1,即可求出解;
(4)方程去分母,移项合并,把m系数化为1,即可求出解;
(5)方程移项合并,把x系数化为1,即可求出解;
(6)方程去分母,移项合并,把x系数化为1,即可求出解.
解答 解:(1)移项合并得:x=-9;
(2)移项合并得:6t=-20,
解得:t=-$\frac{10}{3}$;
(3)去分母得:2-12y=3,
移项合并得:12y=-1,
解得:y=-$\frac{1}{12}$;
(4)去分母得:12-5m=-3m,
移项合并得:2m=12,
解得:m=6;
(5)移项合并得:2x=9,
解得:x=4.5;
(6)去分母得:-16x+4=x,
移项合并得:17x=4,
解得:x=$\frac{4}{17}$.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.下列方程中,解是x=-2的方程是( )
| A. | -2x-1=-5 | B. | 3(x-1)-2=11 | C. | -$\frac{1}{2}$x+1=0 | D. | $\frac{x-1}{3}$+1=0 |
16.下列各题中的变形,属于移项的是( )
| A. | 由2x-2y-1得-1-2y+2x | B. | 由6x-1=x+5得6x-1=5+x | ||
| C. | 由4-x=3x-2得3x-2=4-x | D. | 由2-x=x-2得2+2=x+x |
6.-$\frac{1}{2}$的相反数是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | -$\frac{1}{2}$ |
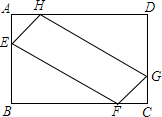 如图,在矩形ABCD中,AB=6,BC=8,点E、F、G、H分别在边AB、BC、CD、AD上,且AE=AH=CF=CG,设AE的长为x,四边形EFGH的面积为S.
如图,在矩形ABCD中,AB=6,BC=8,点E、F、G、H分别在边AB、BC、CD、AD上,且AE=AH=CF=CG,设AE的长为x,四边形EFGH的面积为S.