题目内容
7.勾股定理是几何中的一个重要定理.而在西方,则是由著名数学家毕达哥拉斯用如图①的图形验证了勾股定理.故图①由此得名“毕达哥拉斯树”.图②是由图①放入长方形内得到的,∠BAC=90°,∠ABC=30°,BC=4,D、E、F、G、H、I都在长方形KLMJ的边上,则此长方形KLMJ的面积为( )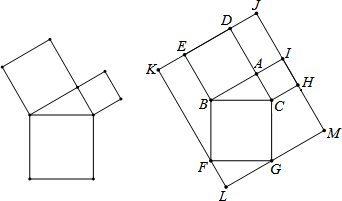
| A. | 48+20$\sqrt{3}$ | B. | 32+20$\sqrt{3}$ | C. | 52+16$\sqrt{3}$ | D. | 28+16$\sqrt{3}$ |
分析 延长AB交KF于点O,延长AC交GM于点P,可得四边形AOLP是正方形,然后求出正方形的边长,再求出矩形KLMJ的长与宽,然后根据矩形的面积公式列式计算即可得解.
解答  解:∵∠BAC=90°,∠ABC=30°,BC=4,
解:∵∠BAC=90°,∠ABC=30°,BC=4,
∴AC=$\frac{1}{2}$BC=2,AB=2$\sqrt{3}$.
如图,延长AB交KF于点O,延长AC交GM于点P,则四边形OALP是矩形.
∵∠CBF=90°,
∴∠ABC+∠OBF=90°,
又∵直角△ABC中,∠ABC+∠ACB=90°,
∴∠OBF=∠ACB,
在△OBF和△ACB中,$\left\{\begin{array}{l}{∠BAC=∠BOF}\\{∠ACB=∠OBF}\\{BC=BF}\end{array}\right.$,
∴△OBF≌△ACB(AAS),
∴AC=OB,
同理:△ACB≌△PGC,
∴PC=AB,
∴OA=AP,
所以,矩形AOLP是正方形,
边长AO=AB+AC=2$\sqrt{3}$+2,
所以,KL=2$\sqrt{3}$+2+2$\sqrt{3}$=4$\sqrt{3}$+2,LM=4+2$\sqrt{3}$,
因此,矩形KLMJ的面积为(4$\sqrt{3}$+2)×(4+2$\sqrt{3}$)=32+20$\sqrt{3}$.
故选:B.
点评 本题考查了勾股定理的证明,作出辅助线构造出正方形是解题的关键.

练习册系列答案
相关题目
16.若x、y为有理数,且m=2x2+9y2+8x-12y+12,则m的值为( )
| A. | 非负数 | B. | 负数 | C. | 正数 | D. | 0 |
16.在面积为60的?ABCD中,过点A作AE⊥直线BC于点E,作AF⊥直线CD于点F,若AB=10,BC=12,则CE+CF的值为( )
| A. | 22+11$\sqrt{3}$ | B. | 22-11$\sqrt{3}$ | C. | 22+11$\sqrt{3}$或22-11$\sqrt{3}$ | D. | 22+11$\sqrt{3}$或2+$\sqrt{3}$ |
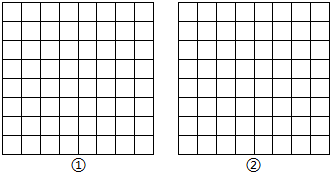 如图,正方形网格中的每一个小正方形的边长都是1,每个小正方形的顶点叫格点,以格点为顶点分别在图①、图②中,画三角形和平行四边形.
如图,正方形网格中的每一个小正方形的边长都是1,每个小正方形的顶点叫格点,以格点为顶点分别在图①、图②中,画三角形和平行四边形. 如图,已知∠1=50°,∠2=130°,且BD∥CE,AC与DF平行吗?为什么?
如图,已知∠1=50°,∠2=130°,且BD∥CE,AC与DF平行吗?为什么?