题目内容
17．某大学为改善校园环境，计划在一块长80米，宽60米的矩形场地中央建一个矩形网球场，网球场占地面积为3500平方米，四周为宽度相等的人行步道，求人行步道的宽度．分析 设出人行横道的宽度，然后根据面积间的关系列出方程求解即可．
解答 解：设人行横道的宽度为x米，根据题意得：（80-2x）（60-2x）=3500
整理得：x2-70x+325=0
解得：x=5或x=65（不合题意，舍去）．
答：人行横道的宽度为5米．
点评 本题考查了一元二次方程的应用，解题的关键是找到等量关系并列出方程．
练习册系列答案
英才计划期末调研系列答案
相关题目
7．对二次函数y=3x2-6x的图象性质，下列说法不正确的是（ ）
| A． | 开口向上 | B． | 对称轴为x=1 | C． | 顶点坐标为（1，-3） | D． | 最小值为3 |
7．勾股定理是几何中的一个重要定理．而在西方，则是由著名数学家毕达哥拉斯用如图①的图形验证了勾股定理．故图①由此得名“毕达哥拉斯树”．图②是由图①放入长方形内得到的，∠BAC=90°，∠ABC=30°，BC=4，D、E、F、G、H、I都在长方形KLMJ的边上，则此长方形KLMJ的面积为（ ）
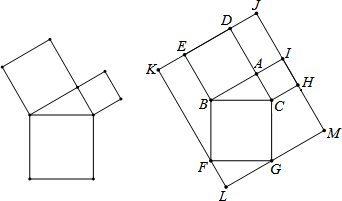
| A． | 48+20$\sqrt{3}$ | B． | 32+20$\sqrt{3}$ | C． | 52+16$\sqrt{3}$ | D． | 28+16$\sqrt{3}$ |
如图，AB∥DE，CM平分∠BCE，CN⊥CM，猜想∠B与∠DCN的数量关系，并说明理由．