题目内容
16.若x、y为有理数,且m=2x2+9y2+8x-12y+12,则m的值为( )| A. | 非负数 | B. | 负数 | C. | 正数 | D. | 0 |
分析 利用配方法将m=4x2+9y2+12xy+8x+12y+3转化为M=(2x+3y+2)2-1的形式,然后根据非负数的性质来求m的值.
解答 解:m=2x2+9y2+8x-12y+12,
=2(x2+4x+4)+9(y2-$\frac{4}{3}$y+$\frac{4}{9}$),
=2(x+2)2+9(y-$\frac{2}{3}$)2,
∵(x+2)2≥0,(y-$\frac{2}{3}$)2≥0,
∴2(x+2)2+9(y-$\frac{2}{3}$)2≥0,即m≥0,
∴m是非负数.
故选:A.
点评 此题考查了配方法的应用、非负数的性质(偶次方),解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
7.对二次函数y=3x2-6x的图象性质,下列说法不正确的是( )
| A. | 开口向上 | B. | 对称轴为x=1 | C. | 顶点坐标为(1,-3) | D. | 最小值为3 |
7.勾股定理是几何中的一个重要定理.而在西方,则是由著名数学家毕达哥拉斯用如图①的图形验证了勾股定理.故图①由此得名“毕达哥拉斯树”.图②是由图①放入长方形内得到的,∠BAC=90°,∠ABC=30°,BC=4,D、E、F、G、H、I都在长方形KLMJ的边上,则此长方形KLMJ的面积为( )
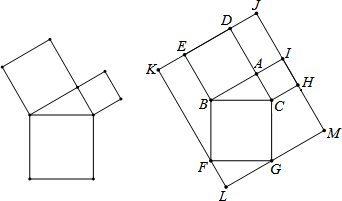

| A. | 48+20$\sqrt{3}$ | B. | 32+20$\sqrt{3}$ | C. | 52+16$\sqrt{3}$ | D. | 28+16$\sqrt{3}$ |
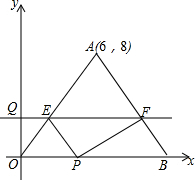 如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0).
如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0).